 Bereiche unterteilt ist:
Bereiche unterteilt ist:
Thermodynamische
Potentiale im Überblick
Enthalpie, freie Enthalpie, innere Energie, freie Energie, Entropie usw. Welches übergeordnete Prinzip steckt dahinter?
| Chemischer Blickwinkel: Reaktion steht bevor. Reaktionen laufen nur dann freiwillig ab, wenn das Potential dabei abnimmt. | Physikalischer Blickwinkel: System im Gleichgewicht | ||||||||
| Bezeichnung, Formelzeichen | Prozessunabhängige Variablen, natürliche Variablen. Variablen, die während des Prozesses konstant bleiben | Rand bedingungen | Ensemble typ | Prozessabhängige Variablen. Variablen, die sich während des Prozesses ändern können | Anmerkungen, praktische Realisierung | Totales Differential | Durch Änderungen welcher
Variablen wird ein neues Gleichgewicht geschaffen |
||
| Innere Energie U | Entropie, Volumen, Teilchenzahl |
S, V, N | Isentrop, Isochor, Teilchenzahl konstant |
SVN | Temperatur, Druck, Chem. Potential |
T, p, µ | Starr begrenztes System, von aussen beheizbar | dU(S,V,N) = TdS + pdV + µdN |
S, V, N |
| Freie Energie F Helmholtz Potential, Kanonisches Potential |
Temperatur, Volumen, Teilchenzahl |
T, V, N | Isotherm, Isochor, Teilchenzahl konstant |
TVN | Entropie, Druck, Chem. Potential |
S, p, µ | Starr begrenztes System im Wärmebad | dF(T,V,N) = -SdT -pdV +µdN |
T, V, N |
| Enthalpie H | Entropie, Druck, Teilchenzahl |
S, p, N | Isentrop, Isobar, Teilchenzahl konstant |
SpN | Temperatur, Volumen, Chem. Potential |
T, V, µ | System in einem Gummiballon, von aussen beheizbar | dH(S,p,N) = TdS + Vdp + µdN |
S, p, N |
| Freie
Enthalpie G Gibbs Energie, |
Temperatur, Druck, Teilchenzahl |
T, p, N | Isotherm, Isobar, Teilchenzahl konstant |
TpN | Entropie, Volumen, Chem. Potential |
S, V, µ | System im Gummiballon in einem Wärmebad. | dG(T,p,N) = -SdT + Vdp + µdN |
T, p, N |
| Grosskanonisches Potential Φ | Temperatur, Volumen, Chem. Potential |
T, V, µ | Isotherm, Isochor, Chemisches Potential konstant |
µVT | Entropie, Druck, Teilchenzahl |
S, p, N | Starr begrenztes System mit einer Öffnung im Wärmebad | T, V, µ | |
| Extensive Grösse | Zugehörige intensive Grösse |
| Volumen
V |
Druck p |
| Entropie
S |
Temperatur T |
| Teilchenzahl
N |
Chem. Potential µ |
Totales
Differential, unabhängige
natürliche Variablen und abhängige Variablen am Beispiel der Freien
Enthalpie G.
Das totale Differential ist eher physikalisch
und weniger chemisch von Bedeutung (die chemische Sichtweise folgt
weiter unten):
mit δ: partielles
Differential, d: vollständiges Differential.
Diese Gleichung gilt für den
Fall, dass das System im Gleichgewicht ist. (T,
p, N) bedeutet, dass diese Grössen für das System als unabhängige
Variablen festgelegt worden sind; die zugehörigen abhängigen
Variablen S, V und N haben sich dann entsprechend eingestellt.
Das System wurde also einmal auf eine bestimmte
Temperatur, Druck und Teilchenzahl als Gleichgewicht "fixiert".
Die partiellen Differentiale sind nichts anderes als
S, V und µ.
Eingesetzt ergibt sich also
dG (T, p, N) = -S*dT + V*dp + µ*dN
Da für G per Definition T, p und N
die unabhängigen Variablen sind, kann man den Wert von G nur ändern,
wenn man T, p oder N ändert, daher tauchen auch gerade diese 3
Variablen als Differentiale auf. Bei den anderen thermodynamischen Potentialen gilt
die selbe Argumentation entsprechend.
Die
chemisch prozesstechnische Sichtweise ist etwas anders.
Zunächst
hat man z.B. 2 getrennte Systeme unterschiedlichen chemischen Inhalts
jeweils im Gleichgewicht. Beide haben eine bestimmte freie Enthalpie.
Dann bringt man beide zusammen, und zwar so, dass sich weder Druck noch
Temperatur ändern können, das Gesamtsystem also eine gute Wärmekopplung
nach aussen hat und atmosphärich offen ist, also eine sehr häufige
anzutreffende prozesstechnische Umgebung. (Die Teilchenzahl N muss man
aufgeben, da sie sich ja durch die Reaktion definitiv ändern kann).
Wenn
die Stoffe der beiden Systeme miteinander reagieren, dann ändert sich
das chemische Potential µ pro Teil, möglicherweise die gesamte Entopie
S und wahrscheinlich auch das gesammte Volumen V. Die unabhängigen
Variablen T
und p haben sich nicht geändert, da die Randbedingungen dementsprechend
beschaffen sind. Damit die Reaktion überhaupt stattfindet, muss die
gesamte Freie Enthalpie kleiner sein als die Summe der freien
Enthalpien der beiden Ausgangssysteme.
Die thermodynamischen
Potentiale unterscheiden sich dadurch, wie sie an die Umgebung gekoppelt sind.
Intuitiv ist klar, dass
bei gleichzeitiger Konstanthaltung einer extensiven Grösse und ihrer zugehörigen
intensiven Grösse sich
auch alle anderen Grössen nicht mehr ändern können. Wenn man
beispielsweise verlangt, dass Druck und Volumen konstant bleiben
sollen, dann kann sich auch sonst keine physikalische Grösse ändern.
Physikalisch
und vor allem chemisch prozesstechnisch interessant sind deshalb diejenigen
Fälle, in denen von allen drei Paaren [extensive Grösse + zugehörige
intensive Grösse] genau ein Element konstant gehalten wird und das
jeweils andere variabel bleiben darf. Dies sind genau diejenigen Fälle, die
für das System maximale Zwangsbedingungen in der Art bedeuten, dass das
System noch allen denkbaren äusseren Einflüssen ausweichen kann.
Beispielsweise
bedeutet konstant gehaltenes Volumen, dass man das System fest
einsperrt. Auf äussere Einflüsse könnte es mit Druckänderung reagieren.
In
der Chemie prozesstechnisch besonders bedeutsam sind Systeme, die mit
der Aussenwelt in zweifacher Hinsicht in Wechselwirkung stehen:
Konstanter Druck und konstante Temperatur, also offene Systeme, die irgendwo herumstehen. Dies beschreibt die freie Enthalpie G,
daher wurde sie weiter oben als Beispiel gewählt.
Insgesamt sind 8 Möglichkeiten denkbar, jeweils ein
Element aus den drei Paaren [extensive
Grösse + zugehörige intensive Grösse] konstant zu halten und das
jeweils andere variabel zu lassen.
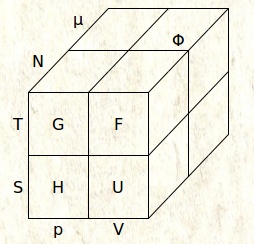
Man kann
dies bildlich anhand eines dreidimensionalen Koordinatensystems
darstellen, wobei jede Achse in 2 Bereiche unterteilt ist:
Bereiche unterteilt ist:
Obere Hälfte: T konstant, Untere
Hälfte: S konstant
Vordere Hälfte: N Konstant, hintere Hälfte: µ konstant
Linke Hälfte: p konstant, rechte
Hälfte: V konstant.
Technisch
bedeutsam sind aber nur diejenigen 4 Möglichkeiten, bei denen sich das
chemische
Potential µ ändern kann (vordere Hälfte), denn nichts anderes sind ja
chemische
Reaktionen.
Physikalisch bedeutsam ist noch das Grosskanonische Potential Φ, hinten rechts oben..