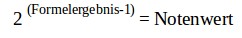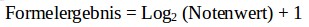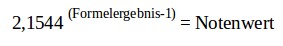
Beispiel 50ct Münze: 2,1544(6-1) = 50
Löst man die Beziehung auf nach dem Formelergebnis, also dem Rang, dann erhält man den Logarithmus:
| Zur Hauptseite ..\..\ |
Zur Themenliste ..\ |
Logarithmus für
Dummies
Es
gibt unterschiedliche Methoden, Zahlen miteinander zu vergleichen, sie
in eine Relation zu setzen. Oft ist es eine Frage der Sichtweise,
meistens aber ergibt sich die "richtige" Methode aus der Natur des
zugrunde liegenden Sachverhaltes.
In diesem Kapitel wird versucht, einen möglichst einfachen Zugang zum
Logarithmus herzustellen, indem bewusst gemacht wird, dass jeder Mensch täglich mit ihm umgeht, ohne es
vermutlich zu merken.
Beispiel 1:
| 1 Packung
Haargummis |
1
Kleinwagen |
|||
| Regulärer
Preis: 2 € |
Sonderangebot: 1 € |
Regulärer
Preis: 10.000 € |
Sonderangebot: 9.999 € |
|
Warum
fühlen wir uns beim Sonderangebot des Kleinwagens veräppelt, wo doch
der eingesparte Betrag derselbe ist wie bei den Haargummis, nämlich 1 €
?
Weil
wir -aus irgend einem Grund- der Ansicht sind, dass nicht die absolute,
sondern die relative Einsparung massgebend ist, also 50% bei den
Haargummis gegenüber lediglich 0,01% beim Kleinwagen. Aber warum
eigentlich?
Hier der Versuch einer Erklärung:
Würden
wir 5.000 Packungen Haargummis bei regulärem Preis kaufen, dann würden
wir genauso viel Geld ausgeben wie für den Kleinwagen, jedoch 5.000 €
gespart gegenüber nur 1 € beim Kleinwagen.
Der
eigentliche Grund ist also, dass wir zuerst die absoluten Preise
vergleichbar machen, und danach erst überlegen, wieviel wir gespart
hätten.
Oder
anders herum: Wollten wir beim Kauf von Kleinwagen 5.000 €
sparen, müssten wir fast 50 Millionen € (für 5.000 Kleinwagen) ausgeben
im Vergleich zu lediglich 5.000 Euro für 5.000 Packungen Haargummis.
Beispiel 2: Geld
Warum gibt es Euro-Währungseinheiten nur in den folgenden
Grössen:
1ct, 2ct, 5ct, 10ct, 20 ct, 50 ct, 1€, 2€, 5€, 10€, 20€,
50€, 100e, 200€, 500 € ?
Man könnte in Analogie zu den Wägestücken früherer
Waagen, wie folgt argumentieren:
"Mit
einer derartigen Staffelung bleibt die Vielfalt der Einheiten
einerseits überschaubar (und ist damit inhärent ein Stück weit
fälschungssicher), andererseits kann man jeden beliebigen Geldbetrag
mit relativ wenigen Einheiten abbilden"
Beispielsweise den Betrag 191,73 € mit 100€ +50€ + 20€ +
20€ + 1€ + 50ct + 20ct + 2ct + 1ct, also insgesamt 9 Einheiten.
Etwas
vereinfacht kann man sagen, dass im existierenden Bargeldsystem die
nächstgrössere Einheit immer den doppelten Betrag aufweist.
Offensichtlich ist das praktisch, denn man kann jeden
beliebigen Betrag ohne besonders nachzurechnen geschwind hinblättern.
Gedanklich läuft das ungefähr so ab:
| Notenwert
[in ct] |
1 |
2 |
5 |
10 |
20 |
50 |
100 |
200 |
500 |
| Formelergebnis |
1 |
1,903 |
3,097 |
4,000 |
4,903 |
6,097 |
7,000 |
7,903 |
9,097 |
| Gerundetes Formelergebnis | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Notenwert [in ct] | 1.000 |
2.000 |
5.000 |
10.000 |
20.000 |
50.000 |
|||
| Formelergebnis | 10,0 |
10,9 |
12,1 |
13,0 |
13,9 |
15,1 |
|||
| Gerundetes Formelergebnis | 10 |
11 |
12 |
13 |
14 |
15 |
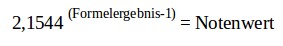
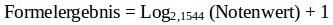
| Notenwert
[in ct] |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
| Formelergebnis | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Notenwert [in ct] | 1.024 |
2.048 |
4.096 |
8.192 |
16.384 |
32.768 |
||||
| Formelergebnis | 11 |
12 |
13 |
14 |
15 |
16 |