Fehlerfortpflanzungsgesetz
mit Beispiel
Siehe auch Toleranzkette.
Obwohl beide Begriffe ein
ähnliches Gebiet
meinen, wird in diesem Glossar auf beide Begriffe separat und in
unterschiedlicher Weise eingegangen.
Beim Fehlerfortpflanzungsgesetz geht es um
Folgendes:
Es werden mehrere Messgrössen gemessen. Jede
Messgrössse sei mit einer Streuung behaftet.
Aus den Messgrössen wird mittels eines
Rechenausdruckes eine Ergebnisgrösse berechnet.
Frage: Welche Streuung hat die Ergebnisgrösse?
Um es vorweg zu nehmen: Mit einfacher Addition
(arithmetisch oder geometrisch) liegt man fast immer falsch.
Das Ergebnis kann optimistisch oder auch pessimistisch
sein.
Um zum Fehlerfortpflanzungsgesetz zu kommen, ist das
Verständnis der Ausgleichsrechnung wichtig.
Die Ausgleichsrechnung behandelt den
Einfluss auschliesslich nicht-systematischer, also zufallsbedingter
Messfehler auf die DIREKTEN Messergebnisse, sowie den daraus
resultierenden Einfluss auf die daraus berechneten INDIREKTEN
Messergebnisse.
Beispiel:
Messung
der Fläche eines Rechtecks. Die Seitenlängen sind die direkten (oder
auch vermittelnden) Messergebnisse, da sie unmittelbar gemessen werden.
Der Flächeninhalt ergibt sich als Rechengrösse indirekt aus dem Produkt
der beiden Seitenlängen.
Die
Messfehler der direkten Messergebnisse (Seitenlängen) wirken sich
"irgendwie" auf das indirekte Messergebnis (Flächeninhalt) aus.
Dies
wird auf mathematische Weise durch das Gauss'sche
Fehlerfortpflanzungsgesetz widergespiegelt (folgt weiter
unten).
Zufallsbedingte und systematische Messfehler
Zufallsbedingte
Messfehler sind solche, auf deren Natur man mit der gegebenen
Messausrüstung keinen Einfluss hat.
Anmerkung: Oder keinen Einfluss nehmen WILL. Das führt
hier
zu weit. Siehe in der Vertiefung der Rubrik
Taguchi: "Störvariable"
Im
Rahmen dieser Messfehler sind die Messungen demnach Resultate von
Zufallsexperimenten.
Beispiele:
Messlatte
kann nicht reproduzierbar an Halterung befestigt werden, Thermometer
ist schwankenden (nicht im Rahmen des Messaufbaus kontrollierbaren)
Bedingungen ausgesetzt (Luftzug, Feuchte,..), der Umfüllprozess bei der
Volumenmessung verläuft manuell und es wird "manchmal etwas"
verschüttet.
Systematische
Messfehler sind solche, die in allen Messungen in gleicher Weise
auftreten, die die Messungen in eine bestimmte Richtung um einen
bestimmten Betrag verfälschen.
Beispiele:
Zu
kurze Messlatte, Thermometer zeigt immer 1 Grad zu wenig an, bei
Volumenmessung wird technisch bedingt immer die selbe Menge
verschüttet.
Wie
man aus zuvor genannten Beispielen sieht, ist die Abgrenzung Zufällige
Messfehler - Systematische Messfehler nicht naturgemäss vorgegeben,
sondern hängt vom Messaufbau und der Messprozedur ab.
Für die Ausgleichsrechnung (oder Fehlerrechnung) sind
ausschliesslich die zufallsbedingten Messfehler von Bedeutung, da nur
sie sich "statistisch" verhalten.
Im Folgenden werden Messfehler als
normalverteilt angenommen.
Normalverteilung ist gleichbedeutend mit der Annahme
sehr vieler zufallsbedingter unabhängiger Einflüsse.
Siehe hierzu auch
zentraler Grenzwertsatz.
Normalverteilte Messergebnisse lassen sich durch einen
Mittelwert
und eine
Standardabweichung beschreiben.
Der Mittelwert ist hierbei der wahrscheinlichste
Messwert, also derjenige Wert, den man erhält, wenn man die Messwerte
aller Wiederholungsmessungen mittelt.
Die Standardabweichung ist die "Streubreite" der bei
den Wiederholungsmessungen generierten Messwerte.
Die Angabe von Messwerten nimmt also folgende Gestalt
an:
Messwert = [Wert] +/- Standardabweichung.
In diesem Intervall liegen etwa 68% aller Messwerte.
Das Gauss'sche Fehlerfortpflanzungsgesetz kommt dann
ins Spiel, wenn man von der Messunschärfe der direkten (oder
vermittelnden) Messergebnisse (~Kantenlängen) auf die Messunschärfe des
daraus gewonnenen indirekten Ergebnisses (~Flächeninhalt) schliessen
will.
Das Gauss'sche Fehlerfortpflanzungsgesetz hat folgende
Gestalt:
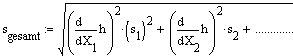 |
Hier bedeuten:
Xi: Direkt zu messende
Messgrössen (grossgeschrieben, weil die Variablen und nicht deren
Realisationen gemeint sind).
si: Die zu den Variablen Xi
gehörenden Standardabweichungen.
h: Die indirekte Messgrösse, also ein
bestimmter funktionaler Zusammenhang der Xi mit der
indirekten Messgrösse.
|
|
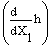 ist die nach dem ersten Glied abgebrochenen
Taylorentwicklung der indirekten Messgrösse h nach der direkten
Messgrösse X1. ist die nach dem ersten Glied abgebrochenen
Taylorentwicklung der indirekten Messgrösse h nach der direkten
Messgrösse X1.
Das Gauss'sche Fehlerfortpflanzungsgesetz ist also
eine Näherung erster Ordnung!
Die Ableitung von h muss an der Stelle xquer
erfolgen.
In die Ableitung von h ist also für X der Wert xquer
einzusetzen.
Entsprechendes gilt für die anderen direkten
Messgrössen Xi.
|
Beispiel
Parallelschaltung von 2 ohmschen Widerständen R1
und R2.
(Bitte ggf. vorab noch einmal zum besseren Verständnis das Ohmsche Gesetz nachlesen).
Messung der beiden einzelnen Widerstände.
R1 = 100 +/-1 Ohm, also s1 = 1 Ohm
R2 = 200 +/- 2 Ohm, also s2 = 2 Ohm
Wie gross ist der Gesamtwiderstand und welche
Standardabweichung hat er?
a) Berechnung des Mittelwertes
Für die Parallelschaltung gilt bekanntlich:
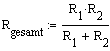 = 66,7 Ohm
= 66,7 Ohm
Rgesamt entspricht h in der Formel des
Gauss'sche Fehlerfortpflanzungsgesetzes.
b) Berechnung der Standardabweichung
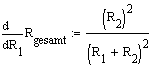 = 0,44
= 0,44
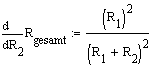 =
0,11 (Beide Ableitungen nach Quotientenregel)
=
0,11 (Beide Ableitungen nach Quotientenregel)
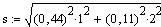 = 0,492
Ohm
= 0,492
Ohm
Ergebnis:
Rgesamt = 66,7 +/- 0,49 Ohm
ist die nach dem ersten Glied abgebrochenen
Taylorentwicklung der indirekten Messgrösse h nach der direkten
Messgrösse X1.