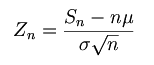
Der
wohl wichtigste Sachverhalt in der
induktiven Statistik.
Der
zentrale Grenzwertsatz ist für das Funktionieren vieler statistischer
Methoden verantwortlich und erleichtert das Treffen von Annahmen
über Verteilungsfunktionen, von denen man entweder gar nicht weiss, wie
sie beschaffen sind oder deren Verteilungsfunktion und die dahinter
stehenden Rechenprozesse sehr langwierig und kompliziert sind.
Der zentrale Grenzwertsatz ist die Hauptursache dafür, dass die Normalverteilung eine herausragende Stellung in der Statistik einnimmt.
Werden aus einer Grundgesamtheit viele Stichproben gezogen, deren Einzelwerte unabhängig und identisch verteilt sind, dann sind die Mittelwerte der Stichproben approximativ normalverteilt,
und zwar unabhängig davon, wie die Verteilungsfunktion der Grundgesamtheit beschaffen ist.
In fast allen praktischen Fällen können die Bedingungen "unabhängig" und "identisch verteilt" gelockert werden:
Die Einzelwerte der Stichproben dürfen schwach abhängig sein.
Die Stichproben können aus unterschiedlichen Verteilungsfunktionen stammen.
Die mathematische Formulierung lautet so:
Sei X1,X2,X3,... eine Folge von Zufallsvariablen, die alle die gleiche Wahrscheinlichkeitsverteilung aufweisen und unabhängig voneinander sind. (Wohlgemerkt: nicht notwendigerweise normalverteilt).
Sei weiter angenommen, dass sowohl der Erwartungswert μ als auch die Standardabweichung σ existieren und endlich sind.
Betrachten wir nun die n-te Teilsumme dieser Zufallsvariablen Sn = X1 + X2 + ... + Xn.
Der Erwartungswert von Sn ist nμ und die Standardabweichung ist σ n½.
Die Verteilung von Sn geht dann für n gegen ∞ gegen die Normalverteilung N(nμ,σ2n),
oder anders formuliert:
Die standardisierte Summe von Sn ,
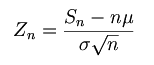
konvergiert die für n gegen ∞ gegen die Standardnormalverteilung N(0,1).
Zur Veranschaulichung des zentralen Grenzwertsatzes siehe diese Exceldatei.
Diese Datei zeigt deutlich, dass selbst für mehrgipfelige Verteilungsfunktionen die Stichprobenmittelwerte normalverteilt aussehen.
Es gibt mehrere spezifischere Formulierungen des zentralen Grenzwertsatzes.
Die bekannteste und fast älteste ist die von Moivre-Laplace: "Die Binomialverteilung ist approximativ normalverteilt"
Mit dem zentralen Grenzwertsatz lassen sich (zusammen mit dem starken Gesetz der grossen Zahlen) auf elegante Weise Vertrauensintervalle für Mittelwerte und Varianzen herleiten.
Da diese ja approximativ normalverteilt bzw. Chi Quadrat verteilt sind, lassen sich die Vertrauensintervalle durch die standardisierte Normalverteilung und die Chi Quadrat Verteilung ausdrücken.
Beispiele:
Vertrauensintervall für den Mittelwert der Poissonverteilung.
Vertrauensintervall für p bei Binomialverteilung.
Siehe auch Extremwert Theorem.
Siehe auch Entropie.