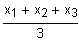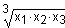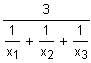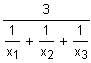Mittelwert Erwartungswert

Allgemeine Bezeichnung für verschiedene Lagemasse.

In den allermeisten Fällen ist der arithmetische Mittelwert oder Erwartungswert gemeint (siehe untenstehende Tabelle).

Die Unterscheidung Mittelwert und Erwartungswert ist nur didaktisch bedeutsam, statistisch gesehen hat sie keine Relevanz.

Der arithmetische Mittelwert ist derjenige Wert eines Datensatzes, bei dem die Summe der Abstandsquadrate zu allen anderen Datenpunkten minimal ist. Man sieht das unmittelbar beispielsweise in der Herleitung der Koeffizienten einer linearen Regressionsgleichung y = ax +b. Siehe dazu Kleinste Quadrate Methode, Abschnitt 1 "Bestimmung der optimalen Modell parameter a und b"  

(Zum Vergleich: Der Median minimiert (mit Einschränkungen) die Summe der absoluten Abstände (nicht quadriert))

Darstellung verschiedener Mittelwerttypen.

Seien x₁, x₂, x₃ Einzelwerte, die gemittelt werden sollen. 

Mittel	Formel	Beispiel	Auf welchem Skalenniveau definiert / nicht definiert?
			Nominal skala	Ordinal skala	Intervall skala	Ratio skala
arithmetisches Mittel		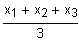Größen, von denen die Summe interpretierbar ist, z. B. von Spielpunkten.
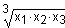geometrisches Mittel		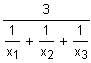Größen, von denen das Produkt anstelle der Summe interpretierbar ist, z. B.  Verhältnisse oder Wachstumsraten.  Logarithmiert man die Einzelwerte und bildet daraus das arithmetische Mittel, dann erhält man den Logarithmus des geometrischen Mittels.
harmonisches Mittel		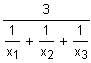Größen, die durch einen Bezug auf eine Einheit definiert sind, z.B.  Geschwindigkeiten (Strecke pro Zeiteinheit), Ernteerträge (Gewicht pro Flächeneinheit), MTBF.  (Also Grössen, bei denen die ausschlaggebende Einheit im Nenner steht)
gewichtetes Mittel	Bezeichnung für alle Mittel, bei denen die Einzelwerte mit (beliebigen) Vorfaktoren multipliziert (gewichtet) werden.	Wird dort verwendet, wo Einzelwerte unterschiedliche Aussagekraft haben, z.B., wenn man die durchschnittliche Schulnote aus mehreren Klassendurchschnitten berechnen will, die Klassen aber unterschiedlich gross sind, oder die einzelnen Klassendurchschnitte als unterschiedlich aussagekräftig betrachtet werden
Des Weiteren sind noch folgende Lagemasse von Bedeutung:
Modalwert	Derjenige Wert, der die grösste Wahrscheinlichkeit hat
Median	Derjenige Wert, der eine Stichprobe in genau 2 Hälften teilt.

Gleitender Mittelwert: Hier werden immer die letzten n Einzelwerte gemittelt. dadurch hinkt die Mittelung zwar immer hinterher, aber der Verlauf wird dadurch glatter.

Tests, die in irgendeiner Form arithmetische Mittelwerte testen, sind beispielsweise:

• t-Test

• ANOVA

• Lineare Kontraste

• Hampel Test  (wenn Ausreisser vermutet werden)

• Fisher Pitman Test

• Fisher Randomisierungstest.

Tests, die in irgendeiner Form Mediane testen, sind beispielsweise:

• Mediantest

• Mann Whitney Test

• Erweiterter Mediantest

• Friedmantest

• Kruskal Wallis Test

• Wilcoxon Vorzeichen Rangtest

Die Angabe des Medians macht gegenüber der Angabe des arithmetischen Mittelwerts dann besonders Sinn, wenn die einzelnen Messwerte sich sehr stark unterscheiden.

Beispiel:

An einer Bushaltestelle stehen 10 Menschen.

Ein Rentner (90 Jahre alt) und 9 Schüler (alle 10 Jahre alt).

Der arithmetische Mittelwert liegt bei (90+9*10)/10 = 18. 

->Niemand aus dieser Gruppe entspricht dieser Altersklasse! 

Der arithmetische Mittelwert würde in diesem Fall dazu verleiten anzunehmen, man hätte es mit einer Gruppe junger Erwachsener zu tun.

Der Median liegt bei 10.

->Dieser Altersklasse entsprechen immerhin 9 von 10 Personen.