ANOVA
Varianzanalyse
Ohne
Frames
Varianzanalyse, Analysis of Variances, oder ANOVA
ist die wichtigste und mächtigste Methode in der Statistik überhaupt.
Design of Experiments, Taguchi, Conjoint Analyse,
Mess-System Analyse usw. sind nichts anderes als spezielle ANOVA.
Grundlegendes Merkmal ist, dass Unterschiede von Mittelwerten
anhand ihrer Varianzen bewertet werden.
Einführende Bemerkungen zur ANOVA.
Zurück zum Glossar
(ANOVA)
ANOVA
Konkrete Zahlenbeispiele mit
expliziter Darstellung aller Rechenschritte befinden sich hier.
Analysis
of Variance, Varianzanalyse.
Auf
dem allgemeinen linearen Modell beruhendes Verfahren.
Modellgleichung: Y= X1 + X2 + ... + Xn.
Die
Ausprägung EINER abhängigen Variablen
Y setzt sich also additiv aus MEHREREN unabhängigen Variablen Xi
zusammen.
Für den Fall mehrerer
abhängiger Variablen siehe MANOVA.
Siehe auch Kovarianzanalyse.
ANOVA ist ein von Ronald Fisher ursprünglich für agrartechnische
Experimente entwickeltes Verfahren, das viele Informationen
gleichzeitig liefert, und mittlerweile in allen wissenschaftlichen
Zweigen Anwendung findet.
ANOVA ist ein statistisches
Auswerteverfahren für Mittelwertvergleiche,
das bei Datenmaterial angewendet wird, welches folgende Eigenschaften
besitzen muss:
-
Messwerte
liegen "sinnvoll" gruppiert (Messwiederholung, der Normalfall)
oder einzeln (keine Messwiederholung, selten) vor.
-
Falls Gruppen:
Jede Gruppe hat ihren eigenen Gruppenmittelwert
-
Alle Gruppen
zusammen haben einen Gesamt-Mittelwert.
-
Die Varianz der Daten ist
überall annähernd gleich (Varianzhomogenität)
-
Messwerte
(unabhängige Variablen) und Zielgrösse (abhängigen Variable) weichen nicht stark von einer
Normalverteilung ab.
-
Zirkularität muss
gegeben sein, wird meistens nicht nachgeprüft.
ANOVA
-
ist ein
Omnibus
Test, das heisst, ANOVA testet das
gesamte Datenmaterial unspezifisch auf einmal.
-
kann als Erweiterung des t-Tests auf mehr als 2 Stichproben angesehen werden.
ANOVA sollte beim Mittelwertsvergleich von mehr als 2 Stichproben
anstelle von wiederholten t-Tests bevorzugt werden. (siehe
multiples
Testen)
ANOVA
vergleicht die Streuung
(genauer gesagt die Varianz) der Stichprobenmittelwerte
mit der Streuung der Stichprobeneinzelwerte innerhalb der
Stichproben.
Man
nennt dies auch Varianzkomponentenzerlegung.
Vereinfacht
kann man sagen:
[Streuung
innerhalb der Gruppen] + [Streuung der Gruppenmittelwerte] = [Gesamte
Streuung].
Als
Ergebnis liefert ANOVA die Information, ob sich die
Stichprobenmittelwerte untereinander
signifikant
unterscheiden.
Die
Funktionsweise von ANOVA wird in folgender Tabelle beispielhaft
ausführlicher erläutert.
|
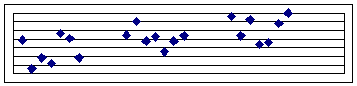
Beispiel 1: Einfaktorielle
ANOVA über 3
Faktorstufen (hier: 3 Stichproben).
-
Es wird nur ein Mass untersucht
-
Zu diesem Mass liegen 3 Stichproben
(Gruppen von Messwerten) vor, jeweils 7 Messungen.
|
|

|
|
|
Die Einzelwerte innerhalb der 3 Gruppen streuen
augenscheinlich weniger als die Mittelwerte der Gruppen.
Die Gruppenmittelwerte unterscheiden sich also
signifikant, d.h.:
Zwischen den einzelnen Gruppen ist irgend etwas "anders".
|
Die Einzelwerte der 3 Gruppen streuen offensichtlich
weiter als die Mittelwerte der Gruppen.
Die Gruppenmittelwerte unterscheiden sich also nicht
signifikant, d.h.: die mit blossem Auge erkennbaren Unterschiede
zwischen den einzelnen Gruppen sind eher zufälliger Natur. Eine andere
Anordnung der Messwerte würde das menschliche Auge möglicherweise zu
anderen Schlussfolgerungen verleiten.
|
Im
obigen Beispiel 1 könnte z.B.der Ernteertrag in Abhängigkeit von in 3
verschiedenen Konzentrationen ausgebrachten Düngers dargestellt
sein.
Während
im linken Bild die Zunahme des Ertrags mit der Düngerkonzentration
offensichtlich scheint, geht dies aus dem rechten Bild nicht so
eindeutig hervor, da es einige Messpunkte gibt, die bei niederer
Konzentration einen höheren Ertrag aufweisen.
Nun
nehmen wir an, wir führen eine Ertragsstudie durch, die ausser der
Düngerkonzentration zusätzlich noch die Menge ausgebrachten Wassers
berücksichtigt.
Wir
betrachten beispielsweise 2 verschiedene Wassermengen und 3
Düngerkonzentrationen.
|
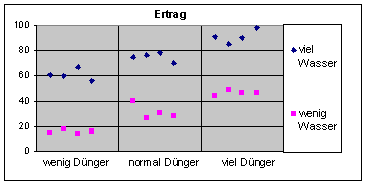
Beispiel 2: Zweifaktorielle
ANOVA über 2
und 3
Faktorstufen.
-
Es werden 2 Masse
untersucht
-
Ein Mass wird auf 2, das andere auf 3 Stufen gemessen,
jeweils 4 Messungen.
Um die Mächtigkeit der ANOVA zu
veranschaulichen, tun wir im Folgenden so, als ob wir bei der selben
Untersuchung 2 verschiedene Ergebnisse erhalten hätten (links und
rechts in folgender Tabelle)
|
|
|
|
|
Die Einzelwerte innerhalb der 3 Gruppen streuen
augenscheinlich weniger als die Mittelwerte der Gruppen.
Die Gruppenmittelwerte unterscheiden sich also
signifikant.
|
| Sowohl viel Wasser als auch viel Dünger
bringen offensichtlich den höchsten Ertrag |
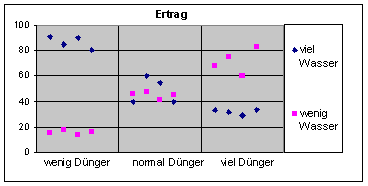
Den höchsten Ertrag bekommt man offensichtlich, wenn
man entweder viel Wasser oder viel Dünger ausbringt, aber
nicht beides.
Hier liegt eine Wechselwirkung von Wasser und Ertrag vor:
- Die vermehrte Zugabe von Wasser
steigert oder senkt den Ertrag , je nachdem ob wenig oder viel Dünger
gegeben wird.
- Die vermehrte Zugabe von Dünger
steigert oder senkt den Ertrag , je nachdem ob wenig oder viel Wasser
gegeben wird.
- Das Gesamt-Optimum scheint bei Zugabe
von wenig Dünger und viel Wasser zu liegen.
|
|
Durch die klassische Methode
"Alle Parameter festhalten und einen Parameter so
lange variieren, bis der Ertrag optimal ist"
hätte man im linken Fall das absolute Optimum
sicherlich gefunden.
Im rechten Fall jedoch wäre das dadurch erreichte
Endergebnis stark abhängig davon, bei welcher Parameterkonstellation
man gestartet wäre:
| Startpunkt bei Parameterkonstellation |
Ermitteltes "Optimum" |
Absolutes
Optimum erreicht? |
| wenig
Dünger, variieren von Wasser |
wenig
Dünger, viel Wasser |
Ja |
| wenig
Wasser, variieren von Dünger |
viel
Dünger, wenig Wasser |
Nein |
| normal
Dünger, variieren von Wasser |
keine
Auswirkung der Wassermenge |
Nein |
| viel
Wasser, variieren von Dünger |
wenig
Dünger, viel Wasser |
Ja |
| viel
Dünger, variieren von Wasser |
viel
Dünger, wenig Wasser |
Nein |
|
|
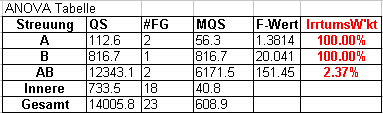
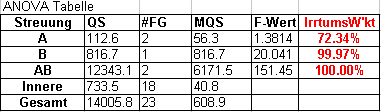
Unten sind die statistischen Auswertetabellen
des obigen Beispiels 2 dargestellt.
|
|
|
|
|
Mit einer
Wahrscheinlichkeit von 100,00% deuten die Messwerte darauf hin, dass
die alleinige Veränderung eines der beiden Parameter Wasser oder Dünger
eine systematische Auswirkung auf den Ertrag hat (Zeilen A und
B).
Achtung, dem zuvor Gesagten liegt der Bayes'sche
Wahrscheinlichkeitsbegriff zugrunde.
Keine Wechselwirkung:
Mit nur 2,37%
Wahrscheinlichkeit deuten die Messwerte darauf hin, dass die
Veränderung eines Parameters die Wirkung des anderen Parameters
beeinträchtigt.
Anders
formuliert: Die Abhängigkeitscharakteristik des Ertrags vom einen
Parameter hängt NICHT grundlegend davon ab, wie der andere Parameter
eingestellt ist.
|
Mit einer
Wahrscheinlichkeit von 72.34 bzw. 99.97% deuten die Messwerte darauf
hin, dass die alleinige Veränderung eines der beiden Parameter Wasser
bzw. Dünger eine systematische Auswirkung auf den Ertrag hat (Zeilen A
und B).
Achtung, dem zuvor Gesagten liegt der Bayes'sche
Wahrscheinlichkeitsbegriff zugrunde.
Wechselwirkung:
Mit 100,0%
Wahrscheinlichkeit deuten die Messwerte darauf hin, dass die
Veränderung eines Parameters die Wirkung des anderen Parameters
beeinträchtigt.
Anders
formuliert: Die Abhängigkeitscharakteristik des Ertrags vom einen
Parameter hängt grundlegend davon ab, wie der andere Parameter
eingestellt ist.
|
Bei
einer mehrfaktoriellen ANOVA (meisstens der Fall) wie im Beispiel 2
veranschaulicht, werden die Stichproben hinsichtlich mehrerer Merkmale gleichzeitig analysiert.
Dabei
gewinnt man zusätzlich Information über mögliche Wechselwirkungen der Faktoren
untereinander
Der
Hauptpluspunkt der ANOVA Vorgehensweise liegt darin, dass Alle Faktoren
sowie eventuelle Wechselwirkungen von Faktoren untereinander
gleichzeitig analysiert werden.
Für
einige Varianzanalysebeispiele siehe folgende Exceldatei
Zurück
19.08.2005





