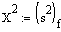
Chi Quadrat Verteilung mit Excel Beispiel

Wichtigste parametrische Verteilungsfunktion in der Statistik. Ein Freiheitsgrad (Parameter). 

Zieht man aus einer standardisierten Normalverteilung (Mittelwert=0 und s=1) f Werte, quadriert diese, summiert auf und teilt durch f , dann ist dieses Ergebnis Chi Quadrat verteilt.

Die Chi Quadrat Verteilung ist also nichts Anderes als die Varianz von Stichproben, die aus einer standardnormalverteilten Grundgesamtheit gezogenen wurden: 

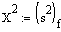
Anmerkung: In mancher Literatur wird unter der X² Verteilung die Quadratesumme verstanden, ohne durch die Anzahl Freiheitsgrade, f, zu teilen. In diesem Glossar wird dies leider nicht einheitlich gehandhabt.

Verallgemeinert auf nicht-standardisierte Normalverteilungen kann man dies wie folgt darstellen: 

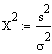
f: Anzahl Werte (Freiheitsgrade) , s²: Varianz der Stichprobe, s²: Varianz der Grundgesamtheit.

Anwendung: 

• Zufallsstreubereich und Vertrauensbereich von Varianzen, 

• Vertrauensbereich des Mittelwertes bei Poissonverteilung

Die Chi Quadrat Verteilung lässt sich mit einer entsprechend skalierten Gammaverteilung geschlossen darstellen

(b = 2 und k = n/2):

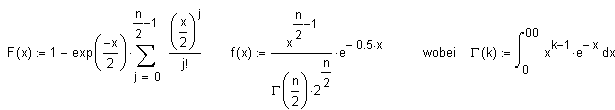
n/2: Anzahl  Freiheitsgrade, b=2: Skalierung.

F: Verteilungsfunktion  Nur für geradzahliges n geschlossen darstellbar.

f: Dichtefunktion  

Erwartungswert	Varianz	Schiefe	Wölbung	Modalwert	Median	Bemerkungen
n	2n		3+12/n	n-2        (n>1)

Für n=2 wird die Chi Quadrat Verteilung zu einer speziellen Exponentialverteilung mit l = 0,5.

In der Zuverlässigkeitstechnik wird die Chi Quadrat Verteilung für MTBF Vertrauensintervalle benötigt.

In dieser Anwendung ist die Chi Quadrat Verteilung aber lediglich eine speziell skalierte Gammaverteilung (für die Zeit bis zum n-ten Ausfall ist ja die Gammaverteilung zuständig).

Die Chi Quadrat Verteilung tritt anstelle der Gammaverteilung nur deshalb in diesem Zusammenhang auf, weil sie historisch schon sehr lange tabelliert vorliegt, und es mathematisch möglich ist, die Gammaverteilung für das spezielle Problem der MTBF (oder Ausfallraten-) Vertrauensintervalle mit der Chi Quadrat Verteilung auszudrücken.

Wie das geht, wird hier skizziert; auf mathematische Exaktheit wird freilich verzichtet.

Für eine zusammenhängende Darstellung der Beziehungen Chi Quadrat Verteilung - t-Verteilung - F-Verteilung - Normalverteilung siehe hier.

Für eine Auflistung der Wechselbeziehungen einiger wichtiger Verteilungsfunktionen siehe hier.

Für eine graphische Darstellung der Chi Quadrat-Verteilung siehe das Arbeitsblatt "Gamma_Chi^2" in dieser Exceldatei.