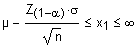
Z1-a: 1-a Quantil der Standardnormalverteilung
s: Standardabweichung der normalverteilten Grundgesamtheit.
n: Stichprobenumfang
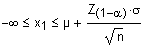
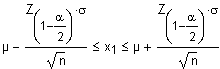
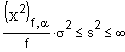
f: Anzahl Freiheitsgrade, = n-1
s: Standardabweichung der normalverteilten Grundgesamtheit.
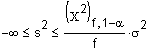
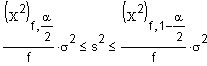
Hier geht es um den Zufallsstreubereich (von einer Grundgesamtheit ausfgehend)
Vorbemerkung:
Vertrauensintervall und Zufallsstreubereich meinen zwar etwas Verschiedenes, bedeuten mathematisch jedoch das Selbe.
Das Vertrauensintervall einer Variablen zur Wahrscheinlichkeit 90% ist der Bereich, in den die Variable mit 90% Wahrscheinlichkeit fällt. Man geht hier von einer Stichprobe aus und schliesst auf die (unbekannte) Grundgesamtheit. Dies ist etwas problematisch und wird in der Rubrik Vertrauensbereich erklärt.
Der Zufallsstreubereich bedeutet das Selbe, allerdings macht er, ausgehend von einer bekannten Grundgesamtheit, Aussagen über eine Stichprobe.
Der Verfasser ist der Ansicht, dass man zwischen den beiden Begriffen Vertrauensintervall und Zufallsstreubereich nicht zu unterscheiden braucht, solange der Kontext (also Stichprobe oder Grundgesamtheit) ersichtlich ist. Dennoch wird das Stichwort Vertrauensbereich in einer separaten Kapitel behandelt, da die Formeln unterschiedlich aussehen.
Aus einer Grundgesamtheit, deren Parameter (z.B.: Mittelwert und Streuung) bekannt sind, wird eine Stichprobe gezogen. Die Parameter der Stichprobe werden meistens nicht genau mit den entsprechenden Parametern der Grundgesamtheit übereinstimmen, sie streuen zufällig in einem gewissen Bereich.
Beispiel: Eine Grundgesamtheit habe den Mittelwert 10 und die Standardabweichung 2.
Bei
5er-Stichproben aus dieser
Grundgesamtheit liegt der
Mittelwert der
Stichproben mit einer
Weitere Beispiele für Zufallsstreubereiche:
| Zufallsstreubereich für: | Formel | Bemerkungen | |
| Mittelwert, bei bekannter Varianz | einseitig unten | 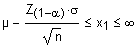 |
µ: Mittelwert
der Grundgesamtheit
Z1-a: 1-a Quantil der Standardnormalverteilung s: Standardabweichung der normalverteilten Grundgesamtheit. n: Stichprobenumfang |
| einseitig oben | 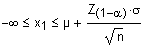 |
||
| zweiseitig | 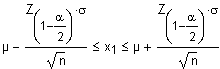 |
||
| Varianz s2 | einseitig unten | 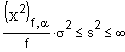 |
X2 f, a a-Quantil
der Chi Quadrat Verteilung
mit f Freiheitsgraden.
f: Anzahl Freiheitsgrade, = n-1 s: Standardabweichung der normalverteilten Grundgesamtheit. |
| einseitig oben | 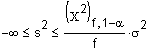 |
||
| zweiseitig | 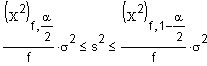 |
||
Siehe auch Vertrauensintervall.