Zur Hauptseite ..\

Statistische Verteilungsfunktionen und ihre Beziehungen zueinender

Die Verteilungsfunktionen der Statistik stehen in Beziehung zueinander. Beispielsweise ist die Normalverteilung eine t-Verteilung für n --> 00. Aber auch Poissonverteilung, Binomialverteilung, Hypergeometrische Verteilung und Normalverteilung lassen sich unter bestimmten Bedingungen ineinander überführen.
Die folgende Übersicht versucht alle Zusammenhänge darzustellen.

Speziell:
Für eine Darstellung der Beziehungen Gammaverteilung - Poissonverteilung - Exponentialverteilung siehe hier.
Dies ist besonders für die Zuverlässigkeitstechnik relevant.

Übersicht über die Wechselbeziehungen einiger kontinuierlicher und diskreter Verteilungsdichtefunktionen

Ausgangsverteilung	Operation	Zielverteilung
Gamma mit der Gamma Funktion		Beta
	b->1/a, k >0 und ganzzahlig	Erlang
	b=2, k=n/2 Siehe auch MTBF Vertrauensintervall	Chi²
	k=1	Exponential
	Integral über x von 0 bis T	Poisson, µ=T/b
		t-Verteilung
		F-Verteilung

*Erlang* mit der Gamma Funktion		Beta
	a->1/b k beliebig	Gamma
	a=1/2, k=n/2	Chi²
	k=1	Exponential
	Integral über x von 0 bis T	Poisson, µ=lT

Weibull Weibullverteilung

h=1

Exponential

h=2

Rayleigh

h=1

l->l/2

x-> |x|

Laplace

Beta Betaverteilung

mit

oder alternativ Betaverteilung Gamma

p=1/2

q=1/2

Arcussinus

p -> 00

q -> 00

(asymptotisch)

Normalverteilung

F-Verteilung

Chi² (n Werte aus Normalverteilung entnommen und quadriert),

oder alternativ Chi Quadrat Gamma mit der Gamma Funktion

und t ein beliebiger Parameter.

n=2

Exponential mit l=1/2

Quotient zweier C²Verteilungen mit n und m Freiheitsgraden, n>m.

F-Verteilung (n,m)

*Exponential*	k-fache Faltung	Gamma (k) -> Exponential
	k-fache Faltung	*Erlang* (k) -> Exponential
	l->l/2 x-> \|x\|	Laplace
	Diskretisierung	Geometrische Verteilung

*t-Verteilung* (n Werte aus Normalverteilung entnommen) oder alternativ mit der Gamma Funktion	n=1	Cauchyverteilung
	n -> 00	Normalverteilung
	= *F-Verteilung*: F_(1,n)

*Hypergeometrische Verteilung*	n -> 00 d -> 0 p=d/N (asymptotisch)	Binomialverteilung
Binomialverteilung	n -> 00 p -> 0 np=µ (asymptotisch)	Poisson
	n=1	Bernoulliverteilung
	np(1-p) >9 (asymptotisch)	Normalverteilung
Poissonverteilung	µ > 9 (asymptotisch)	Normalverteilung
Negative Binomialverteilung	n=1	Geometrische Verteilung
Negative Binomialverteilung	n(1-p)=µ n -> 00 (asymptotisch)	Poisson
Normalverteilung	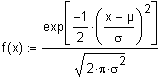x -> ln(x)	Lognormalverteilung

*F-Verteilung* F(m,n)		Quotient zweier *Chi Quadrat Verteilungen*
*F-Verteilung* F(m,n)	m -> unendlich	*Chi Quadrat Verteilung* X²_n
*t-Verteilung*	Quadrieren	*F-Verteilung* F_(1,m) (Normalverteilung)²/ *Chi Quadrat Verteilung*
Normalverteilung	Quadrieren	F-Verteilung F_{(1,unendlich)}

Zurück zum Glossar (Verteilungsfunktion)

13.09.2005

Datenschutzhinweise