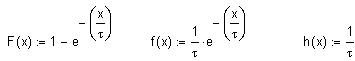
Exponentialverteilung
Die Exponentialverteilung ist die Wahrscheinlichkeitsverteilung der Zeit zwischen 2 Ereignissen bei
Homogenem Poisson Prozess ( HPP) (also konstanter Ausfallrate).
Liegt allen elektronischen Zuverlässigkeitsberechnungsstandards zugrunde.
Die Exponentialverteilung ist gemäss dem Prinzip maximaler Entropie die passende Verteilungsfunktion für die technische Situation
"Wir kennen nur den Mittelwert und wissen sonst (insbesondere Standardabweichung) nichts".
Siehe auch Punkt 4 am Ende der Rubrik Normalverteilung.
Dort wird ein Zusammenhang zum Maximum Entropie Prinzip erwähnt.
Die k-fache Faltung der Ableitung der Exponentialverteilung, also der Wahrscheinlichkeitsdichtefunktion, ergibt die Gamma Verteilung mit Formparameter b=1 und Skalen parameter l (oder 1/t).
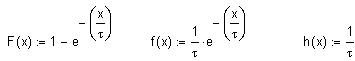
F: Verteilungsfunktion, f: Dichtefunktion, h: Ausfallratenfunktion ,
| Erwartungswert | Varianz | Schiefe | Wölbung | Modalwert | Median | m-tes Moment |
 |
 |
2 | 9 | 0 |  |
 |
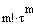Anwendungsbeispiel aus der Zuverlässigkeitstechnik:
Hat man bei einer bestimmten kumulierten Testdauer genau n Ausfälle festgestellt, dann gilt für die obere Vertrauensgrenze der Ausfallrate zum Vertrauensniveau 1-alpha:
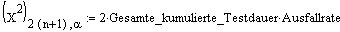, bzw. 
also:
Die doppelte gesamte Testdauer geteilt durch die Mittlere Zeit zwischen 2 Ausfällen ( MTBF) ist Chi Quadrat verteilt mit 2n Freiheitsgraden. n ist die Anzahl festgestellter Ausfälle.
[Anmerkung: (n+1) gilt bei zeitbegrenztem Testen. Bricht man den Test geplant nach dem n-ten Ausfall ab (fehlerbegrenztes Testen), dann gilt n statt (n+1)]
Eine zu dieser Methode alternative Methode für den (häufigen!) Spezialfall Null Ausfälle heisst Erfolgslaufmethode und wird in dieser Exceldatei veranschaulicht: Erfolgslaufmethode.
Beispiel (siehe auch Operationscharakteristik, im 2. Teil ist das selbe Beispiel dargestellt)
Wir testen 20 h lang und stellen dabei z.B. 90 Ausfälle fest.
Der Schätzwert für die Ausfallrate liegt also bei 90/20h = 4,5/h.
Bei genau 90 Fehlern beträgt die Wahrscheinlichkeit, dass die Ausfallrate grösser ist als 5/h nach einsetzen in obige Formel:
.
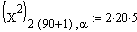Man beachte, dass a die gesuchte Grösse ist.
Mit der Excelfunktion CHIVERT(2*20*5;2*91) ergibt sich der Zahlenwert 17,14%.
Mit einer Wahrscheinlichkeit von 17,14% kann man bei dem vorliegenden Testergebnis (90 Ausfälle/20h) behaupten, dass die "wahre" (aber unbekannte) Ausfallrate grösser ist als 5/h.
Für den Fall, dass während des gesamten Tests kein einziger Ausfall aufgetreten ist, existiert eine Approximationsformel.
Ein Vergleich dieser Approximationsformel mit der zuvor beschriebenen Chi Quadrat Formel befindet sich hier.
Vertiefung: Wie kommt es zu der Formel für die Vertrauensintervalle?
Für eine Darstellung der Beziehungen Gammaverteilung - Poissonverteilung - Exponentialverteilung siehe hier.
Für die allgemeine Bestimmung des "optimalen" Parameters einer exponentialverteilten Stichprobe sowie weitere zuverlässigkeitsrelevante Betrachtungen siehe Beispiel 4 unter Maximum Likelihood Estimation (MLE).
Siehe auch Arrheniusgleichung.
Siehe auch Weibullanalyse.