Die ersten 4 Momente einer Dichtefunktion und davon abgeleitete Grössen
Die zentralen Momente einer Verteilungsfunktion kann man etwas salopp formuliert als Taylor-Entwicklung der Dichtefunktion um den Mittelwert µ ansehen.
Das k-te Moment ist definiert zu:
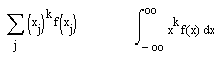im diskreten bzw.
kontinuierlichen Fall.
Für "x" wird bei höheren
Momenten (x-µ) bzw. (x-µ)/
Höhere Momente werden also mit den ersten beiden Momenten skaliert.
1.
k=1
Das erste Moment einer Verteilungsfunktion ist gleich dem Erwartungswert E(x) der zentrierten Variablen (x-µ) und berechnet sich zu:
Der Erwartungswert ist also das gewichtete Mittel von
X, wobei die Gewichtung jeweils mittels der entsprechenden
Schreibt man (x-µ) statt x , dann erhält man das erste zentrale Moment, welches definitionsgemäss = 0 ist.
2.
Streuung
k=2
Das zweite, zentrale Moment, die Varianz Var(x), ist gleich dem Erwartungswert der 2. Potenz der zentrierten Variablen (x-µ),
ist der wichtigste Streuungs parameter einer Verteilungsfunktion und berechnet sich zu:
Die Varianz ist also das gewichtete Mittel über die quadratischen Abweichungen von X vom Erwartungswert, wobei die Gewichtung jeweils mittels der entsprechenden Wahrscheinlichkeit erfolgt,
Die Standardabweichung ergibt sich aus der Wurzel der Varianz.
3.
k=3
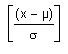
und berechnet sich zu:
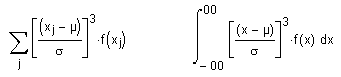
Die Schiefe wird oft als Mass für die Schiefe einer Verteilungsfunktion herangezogen, obwohl das 5., 7. usw. zentrale Moment ebenfalls zur Schiefe beitragen.
4.
Wölbung
k=4
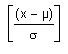
und berechnet sich zu:
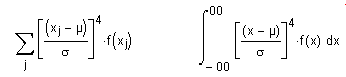
Die Wölbung wird oft als Mass für die "Flachheit" einer Verteilungsfunktion herangezogen, obwohl das 6.,8,. usw. zentrale Moment ebenfalls zur Flachheit beitragen. Eine weitere gebräuchliche Grösse für die Wölbung ist der Exzess.
Exzess = Kurtosis -3.
Die Standardnormalverteilung hat die Kurtosis 3, folglich den Exzess 0.