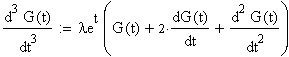Momentenerzeugende
und Charakteristische Funktion mit Beispielen
Mittelwert,
Varianz, Schiefe von Binomialverteilung und Poissonverteilung
Ohne Frames
Charakteristische
Funktionen oder Momentenerzeugende Funktionen werden benötigt, um die
Momente von Verteilungsfunktionen herzuleiten, also z.B. Mittelwert,
Varianz, Schiefe bzw. Kurtosis, Wölbung bzw. Exzess. Diese
Funktionen erzeugen etwas; sie sind ein Kunstgriff aus der Mathematik
und machen gewisse
Umformungsschritte erst möglich.
zurück
zum Glossar (momentenerzeugende
Funktion)
Charakteristische Funktion
Fouriertransformierte
einer
Wahrscheinlichkeitsverteilung.
Rechenhilfe
zur einfachen Berechnung der Momente einer
Verteilungs(Dichte-)Funktion.
Hierzu
gebräuchlich ist auch die momentenerzeugende Funktion.
2
Beispiele
zur Berechnung diverser Momente mit Hilfe der momentenerzeugenden
Funktion
1.)
Binomialverteilung
1.a)
Berechnung der momentenerzeugenden Funktion
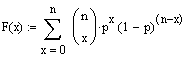
Der
Erwartungswert
von 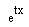 lautet dann:
lautet dann:
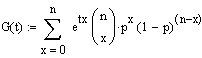 <=>
<=> 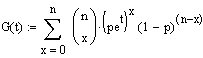 <=>
<=> 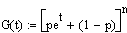
Der
letzte
Umformungsschritt folgt direkt aus dem binomischen Lehrsatz
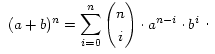
1.b)
Berechnung des
Mittelwertes
Das
erste
Moment berechnet sich mittels der ersten Ableitung nach t zu: 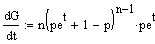
mit
t=0 ergibt
sich: 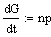 ,
,
also
Mittelwert
= np.
1.c)
Berechnung der Varianz
Das
zweite
Moment berechnet sich zu:
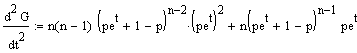 <=>
<=> 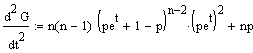
mit
t=0 ergibt
sich:
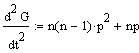
Mit
der unter
Varianz
angegebenen Formel
 ergibt sich
ergibt sich
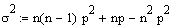 = np(1-p),
= np(1-p),
also
Varianz =
np(1-p).
2.)
Poissonverteilung
2.a)Berechnung
der momentenerzeugenden Funktion
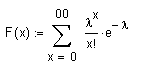
Erwartungswert
von
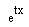 :
:
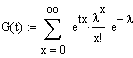 <=>
<=> 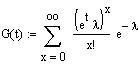 <=>
<=> 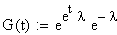
2.b)
Berechnung des Mittelwertes
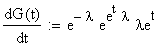 mit t=0 ergibt sich
mit t=0 ergibt sich 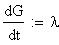 ,
,
also
Mittelwert
= 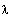
2.c)
Berechnung der Varianz
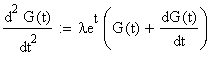 mit t=0 ergibt sich
mit t=0 ergibt sich 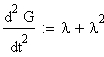 ,
,
mit
der bei Varianz
angegebenen Formel
 ergibt sich
ergibt sich
Varianz
= 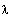
2.d)
Berechnung der Schiefe
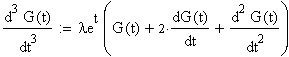
mit
t=0 und der bei
Schiefe
und Varianz
angegebenen Formeln

bzw.

ergibt
sich nach mehreren Umformumngsschritten
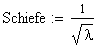
zurück
zum Glossar (momentenerzeugende
Funktion)
21.08.2005
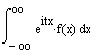
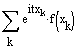
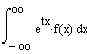
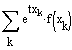
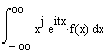
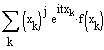
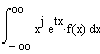
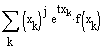
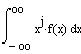
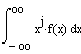
![]() bzw.
bzw. ![]() =1.
=1. ![]() bzw.
bzw. ![]() implizierten Umformungsschritte, ja sogar überhaupt nicht
zu den j-ten Momenten gekommen wäre.
implizierten Umformungsschritte, ja sogar überhaupt nicht
zu den j-ten Momenten gekommen wäre.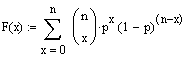
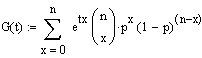 <=>
<=> 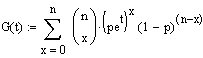 <=>
<=> 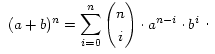
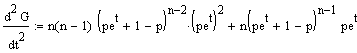 <=>
<=> 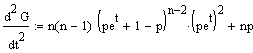
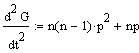
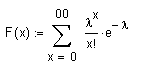
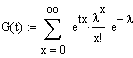 <=>
<=> 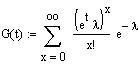 <=>
<=> 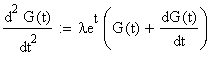 mit t=0 ergibt sich
mit t=0 ergibt sich 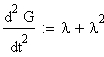 ,
,