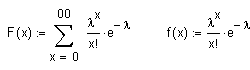
Poissonverteilung

Die Poissonverteilung dient zur Beschreibung der Anzahl Ereignisse pro Intervall bei einem Poisson Prozess, 

also z.B. des Sachverhaltes 

• "Anzahl Fehler/Einheit",

• "Anzahl Ereignisse/Zeiteinheit". 

Siehe zur Abgrenzung auch Binomialverteilung: "Anzahl fehlerhafter Einheiten"  

Die Poissonverteilung besitzt nur 1 Parameter, der sowohl Erwartungswert, als auch Varianz ist. 

F: Verteilungsfunktion: 

f: Dichtefunktion

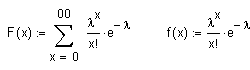
Erwartungswert	Varianz	Schiefe	Wölbung	Modalwert	Median	Bemerkungen
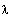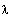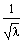						2. Moment:

Zahlenbeispiel:

Pro Stunde ereignen sich im Mittel 25 Telefonanrufe. Wie gross ist die Wahrscheinlichkeit P₃₀, dass in einer bestimmten Stunde

a) höchstens 30,  b) genau 30, c) mindestens 31 Anrufe eintreffen?

Zu a) l = 25; x = 30 Mit der Excelfunktion POISSON(30;25;wahr) ergibt sich P_{max 30} = 0,863

Zu b) l = 25; x = 30 Mit der Excelfunktion POISSON(30;25;falsch) ergibt sich P₌₃₀ = 0,045

Zu c) l = 25; x = 30 Mit der Excelfunktion [1-POISSON(30;25;wahr)] ergibt sich P_{min 31} = 0,137

Weitere Zahlenbeispiele siehe unter Chernoff Ungleichung.

Die Poissonverteilung ist das Integral der Gammaverteilung über die Zeit. Der Formparameter der Gammaverteilung entspricht dem Mittelwert der daraus resultierenden Poissonverteilung.

Das in der Literatur oft genannte Attribut "Für seltene Ereignisse" ist falsch und irreführend, denn die Poissonverteilung ist eine eigenständige Verteilung für einen eigenständigen Sachverhalt, nämlich der Anzahl Ereignisse pro Intervall bzw. der Anzahl Fehler pro Einheit. Ob es sich um seltene Fehler oder Ereignisse handelt ist für die Poissonverteilung völlig bedeutungslos. 

Ausserdem enthält der Begriff "selten" keinerlei quantitatives Mass.

Richtig ist, dass man die Poissonverteilung aus rechentechnischen Gründen (also näherungsweise) an Stelle der Binomialverteilung nehmen kann, wenn die Wahrscheinlichkeit p klein ist und die Anzahl n gross. Siehe dazu hier.  

Zur graphischen Berechnung von Vertrauensintervallen der Poissonverteilung siehe Thorndike Nomogramm oder allgemein Nomogramm.

Für eine graphische Veranschaulichung der Beziehungen 

Hypergeometrische Verteilung - Binomialverteilung - Poissonverteilung - Normalverteilung 

in Excel siehe hier.

Für eine mathematische Darstellung der selben Beziehungen siehe hier.

Dort sind auch die Bedingungen genannt, ab wann eine Verteilung durch eine andere genähert werden darf.

Für eine Darstellung des zuverlässigkeitstechnisch interessanten Beziehungsdreiecks Gammaverteilung - Poissonverteilung - Exponentialverteilung siehe hier.

Für eine Auflistung der Wechselbeziehungen einiger wichtiger Verteilungsfunktionen siehe hier.

Zur Herleitung von Mittelwert und Varianz der Poissonverteilung siehe Charakteristische Funktion. 

Für die Bestimmung des "optimalen" Parameters l einer poissonverteilten Stichprobe siehe Beispiel unter Maximum Likelihood Estimation (MLE). 

Siehe auch Design eines zweiseitigen Stichprobentests als Beispiel 

Vertrauensintervall

In dieser Unterrubrik ist skizziert, wie es zu der Formel

kommt. Diese Formel liefert das einseitige Vertrauensintervall für eine in einem Test ermittelte MTBF. 

Die Chi Quadrat -Verteilung kommt dadurch ins Spiel, dass man die "für dieses Problem eigentlich zuständige" Gammaverteilung (die Verteilung der Anzahl Ausfälle pro gegebener Zeit) durch mathematische Tricks so hinskaliert, dass eine Chi Quadrat Verteilung, (dargestellt als Gammaverteilung), herauskommt. 

Bei der Berechnung des Vertrauensintervalls der Poissonverteilung kann man wieder von obiger Formel ausgehen, wenn man bedenkt, dass die gesamte kumulierte Testdauer geteilt durch die MTBF ja gerade die Anzahl Fehler pro gegebener Zeit ist, und diese ist ja bekanntermassen poissonverteilt. 

Die rechte Seite der obigen Gleichung ist also poissonverteilt, und links steht eine Chi Quadrat Verteilung. 

Somit ist der Bezug zur Chi Quadrat Verteilung als Vertrauensintervall der Poissonverteilung hergestellt: 

Als einseitige untere Vertrauensgrenze für die Poissonverteilung ergibt sich somit:

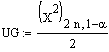, und als obere einseitige Vertrauensgrenze entsprechend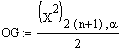

Will man das zweiseitige Vertrauensintervall, dann kommen beide Formeln gleichzeitig zum Einsatz und es muss beidesmal a/2 statt a heissen.

Anwendungsbeispiel aus der Zuverlässigkeitstechnik

Bei einem Test mit vorgegebener Dauer sind 10 Einheiten ausgefallen. 

Wie viele Teile werden bei einer Wiederholung dieses Tests mit einer Wahrscheinlichkeit von 90% (-> a = 10%) höchstens ausfallen? 

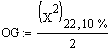= 15,4. Dies kann man mit der Excelfunktion [CHIINV(0.1;22)]/2 nachrechnen. 

Fragte man nach der unteren Vertrauensgrenze, so ergibt sich 

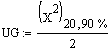= 6,2. (Entsprechend [CHIINV(0.9;20)]. 

Fragte man nach dem zweiseitigen 90% Vertrauensintervall, so ergeben sich 5,4 und 17,0. 

In den nun gleichzeitig anzuwendenden Formeln muss man dann statt 10% und 90% nun 5% und 95% angeben.