zurück zum Glossar (Nomogramm)
Graphisches Hilfsmittel zur Berechnung von in der Regel schwierigen, nichtlinearen Formeln.
Nomogramme bestehen meisst aus einem "krummen" Rasternetz.
Auf dieses Rasternetz legt man auf bestimmte Weise ein Lineal und liesst den interessierenden Wert mehr oder weniger direkt ab.
Auch im Zeitalter moderner Rechner und Software sind Nomogramme immer noch das schnellste Mittel.
Die beschränkte Genauigkeit reicht für die meisten praktischen Zwecke aus.
Beispiele für Nomogramme:
Clopper-Pearson (Binomialverteilung)
22.01.2006
zurück zum Glossar (Nomogramm)
zurück zum Glossar (Larson Nomogramm)
Graphisches Diagrammnetz zur Ermittlung von Quantilen der (kumulierten) Verteilungsfunktion bei Binomialverteilung. Pendant zum Wilrich Nomogramm (Normalverteilung), und Thorndike Nomogramm (Poissonverteilung)
Anwendung z.B. bei
Design von Stichprobenplänen (Siehe auch Operationscharakteristik)
Bestimmung von Zufallsstreubereichen
Bestimmung von Vertrauensintervallen
Ausführliche Beispiele siehe hier
Siehe auch Wilrich Nomogramm
Siehe auch Clopper-Pearson Nomogramm
Siehe auch Durrant Nomogramm
27.08.2005
zurück zum Glossar (Larson Nomogramm)
zurück zum Glossar (Thorndike Nomogramm)
Graphisches Diagrammnetz zur Ermittlung von Quantilen der (kumulierten) Verteilungsfunktion bei Poissonverteilung. Pendant zum Wilrich Nomogramm (Normalverteilung) und Larson Nomogramm (Binomialverteilung)
Anwendung bei
Bestimmung von Vertrauensintervallen
Bestimmung von Zufallsstreubereichen
Design von Stichprobenplänen (Siehe auch Operationscharakteristik)
Ausführliche Beispiele siehe hier
Siehe auch Wilrich Nomogramm
Siehe auch Clopper-Pearson Nomogramm
Siehe auch Durrant Nomogramm
30.08.2005
zurück zum Glossar (Thorndike Nomogramm)
zurück zum Glossar (Wilrich Nomogramm)
Pendant zum Larson Nomogramm (Binomialverteilung), jedoch für normalverteilte Merkmalswerte.
Es gibt verschiedene Varianten des Wilrich-Nomogramms:
Stichprobenanweisung: (xquer, s) {Standardabweichung bekannt}
Stichprobenanweisung: (xquer, s) {Standardabweichung unbekannt}
Abgrenzungsfaktor für xquer - Annahmekarte (oft mit Regelkarte verwechselt)
Abgrenzungsfaktor für xschlange - Annahmekarte (Median)
Abgrenzungsfaktor für Urwertkarte
Zu den letzten 3 Punkten siehe auch die Anmerkungen in der detaillierten Einführung in SPC, ganz unten.
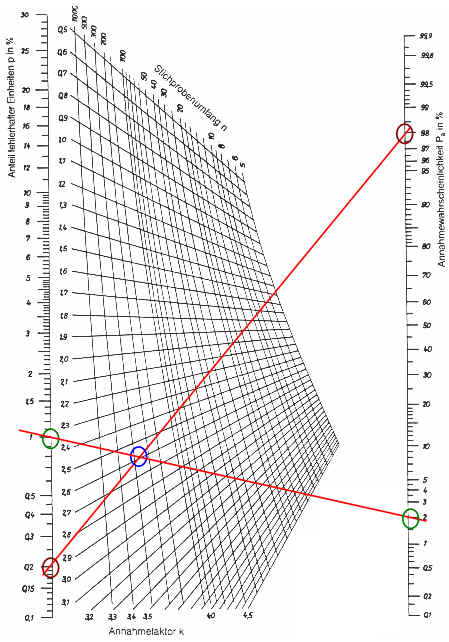
Beispiel 1
Stichprobenanweisung (xquer,s)
(die Stichprobenanweisung (xquer,s) funktioniert analog mit einem geringfügig anders aussehenden Nomogramm).

Erläuterung:
Dargestellt ist das Wilrich Nomogramm (xquer,s).
Es soll eine Stichprobenanweisung generiert werden mit den folgenden Eigenschaften
(siehe auch Operationscharakteristik):
Lose mit einem (geringen) Fehleranteil von 0.2% sollen mit 98% Wahrscheinlichkeit angenommen werden, also mit nur 2 % Wahrscheinlichkeit fälschlicherweise zurückgewiesen werden.
(braune Kreise)
Lose mit einem (hohen) Fehleranteil von 1% sollen mit nur 2 %Wahrscheinlichkeit irrtümlicherweise angenommen werden, also mit 98% Wahrscheinlichkeit zurückgewiesen werden.
(grüne Kreise)
Die beiden durch jeweils farbgleich markierte Punkte gehenden Geraden (rot) schneiden sich im Nomogramm in einem Punkt (blauer Kreis).
Dieser Punkt fällt zwar nicht genau auf einen Rasterpunkt, entspricht aber ungefähr n = 250 und k = 2,6.
--> Damit die Stichprobenanweisung die oben genannten Kriterien erfüllt, muss der Stichprobenumfang ca. 250 betragen, und der aus den 250 Werten berechnete Mittelwert muss mindestens um das 2,6-fache der aus den 250 Werten berechneten Standardabweichung von der nächsten Toleranzgrenze entfernt liegen.
Beispiel 2
Abgrenzungsfaktor für xquer -Regelkarte.
Es soll eine Regelkartenvorschrift ermittelt werden, die bei einem wahren (aber unbekannten) Fehleranteil von 1% zu einer Eingriffswahrscheinlichkeit von 99% führt. (Siehe auch Operationscharakteristik)
Wenn also der wahre Fehleranteil bei 1% liegen sollte, dann will man dies mit einer einzigen Stichprobe erkennen.

Erläuterung:
Dargestellt ist das Wilrich Nomogramm für den Abgrenzungsfaktor einer xquer Regelkarte.
Die rote Linie geht durch den 1%-Punkt der Skala für den momentanen Fehleranteil (links) und durch den 99%-Punkt der Eingriffswahrscheinlichkeit (rechts).
Diese Linie schneidet das Nomogramm in vielen Wertepaaren (Stichprobenumfang | Abgrenzungsfaktor).
Grüne Linien:
Wählt man den Stichprobenumfang zu 5 (kleine Stichprobe), dann muss der aus den 5 Werten berechnete Mittelwert mindestens um das 3,4-fache der aus den 5 Werten berechneten Standardabweichung von der nächsten Toleranzgrenze entfernt liegen. Tut er das nicht, dann muss eingegriffen werden.
Blaue Linien:
Bei einem Stichprobenumfang von n=20 ergibt sich entsprechend ein Abgrenzungsfaktor von 2,85.
Braune Linie:
Einen wahren Fehleranteil von 0,5% erkennt eine Stichprobe vom Umfang n=20 "nur" noch mit 88% Wahrscheinlichkeit.
30.01.2006
zurück zum Glossar (Wilrich Nomogramm)
zurück zum Glossar (Durrant Nomogramm)
Graphisches Hilfsmittel zur Bestimmung des Vertrauensbereiches des Überschreitungsanteils bei normalverteilten Merkmalen.
Beispiel
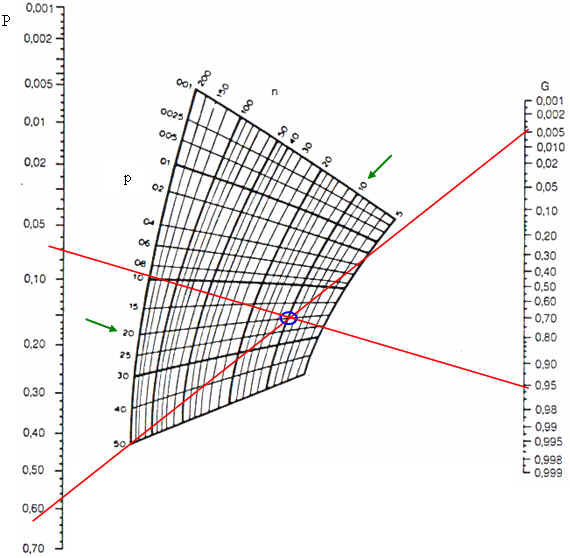
Erläuterung:
Dargestellt ist das Durrant Nomogramm.
In einer Stichprobe des Umfangs n=10 (grüner Pfeil) wurde ein Überschreitungsanteil von p= 0,2 bzw. 20% (grüner Pfeil) gefunden.
Es soll der zweiseitige 90%- Vertrauensbereich des Überschreitungsanteils der Grundgesamtheit ermittelt werden.
Die beiden Linien n=10 und p=20% schneiden sich (blauer Kreis).
Von der rechten Skala G sind von den Punkten 0,05 und 0,95 Geraden durch den mittels blauen Kreises markierten Punkt zu legen.
Die Schnittpunkte der roten Linien mit der linken Skala P bilden die Grenzen des gesuchten Vertrauensbereiches.
PGrundgesamtheit, oben ~ 0.57
pGrundgesamtheit, unten ~ 0.07
--> Der "wahre", aber unbekannte Überschreitungsanteil der normalverteilten Grundgesamtheit liegt mit 90% Wahrscheinlichkeit zwischen 0.07 und 0.57, wenn man mit einer Stichprobe des Umfangs n = 10 einen Überschreitungsanteil von 0.2 ermittelt hat.
Dieser Formulierung liegt der Bayes'sche Wahrscheinlichkeitsbegriff zugrunde.
30.01.2006
zurück zum Glossar (Durrant Nomogramm)
zurück zum Glossar (Clopper-Pearson Nomogramm)
Graphisches Hilfsmittel zur Bestimmung des Vertrauensbereiches der relativen Häufigkeit P in einer binomialverteilten Grundgesamtheit.
Das leistet das Larson Nomogramm zwar auch, nur etwas "umständlicher".
(Dafür ist das Larson Nomogramm aber vielseitiger einsetzbar)
Ausgehend von einer Stichprobe des Umfangs n, für die die relative Häufigkeit p ermittelt wurde, schliesst man auf die "wahre", aber unbekannte relative Häufigkeit in der Grundgesamtheit.
Mit Hilfe von n und p ermittelt man mit dem Clopper-Pearson Nomogramm graphisch den Vertrauensbereich P zu einem gegebenen Vertrauensniveau (1-a).
Clopper-Pearson Nomogramme sind für verschiedene (1-a) erhältlich, beispielsweise für 95% und 99%.
Beispiel
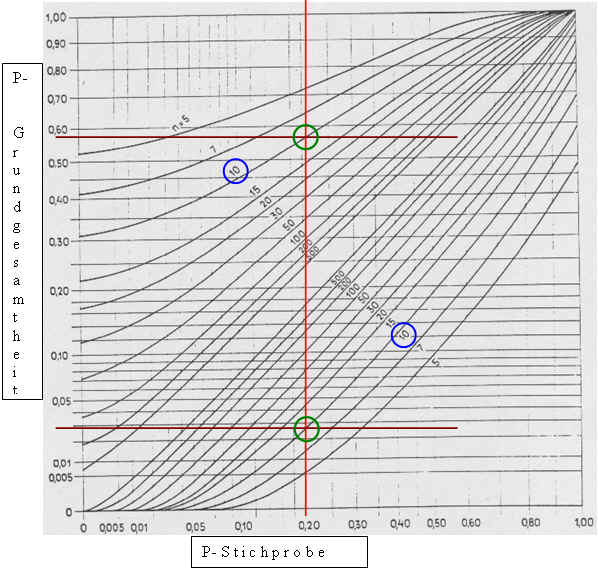
Erläuterung:
Dargestellt ist das Clopper-Pearson Nomogramm für das zweiseitige Vertrauensniveau 1-a = 95%.
In einer Stichprobe des Umfangs n=10 (blaue Kreise) wurde ein relativer Fehleranteil von 0,2 (rote Linie). gefunden.
Die beiden zu n=10 gehörenden Nomogrammlinien schneiden sich mit der roten Linie (grüne Kreise).
Die horizontalen Projektionen dieser beiden Schnittpunkte zur linken Achse (braune Linien) ergeben die beiden 95% Vertrauensgrenzen des Fehleranteiles der zu der Stichprobe gehörenden Grundgesamtheit.
PGrundgesamtheit, oben ~ 0.58
pGrundgesamtheit, unten ~ 0.03
--> Der "wahre", aber unbekannte Fehleranteil der binomialverteilten Grundgesamtheit liegt mit 95% Wahrscheinlichkeit zwischen 0.03 und 0.58, wenn man mit einer Stichprobe des Umfangs n = 10 einen Ausschussanteil von 0.2 ermittelt hat.
Dieser Formulierung liegt der Bayes'sche Wahrscheinlichkeitsbegriff zugrunde.
Anmerkung:
Alles zuvor Beschriebene leistet das Larson Nomogramm auch, nur etwas "umständlicher", dafür ist es aber vielseitiger.
29.01.2006
zurück zum Glossar (Clopper-Pearson Nomogramm)