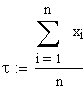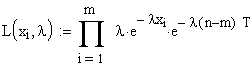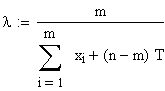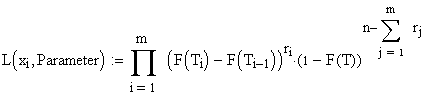Maximum
Likelihood Methode
Schätzung
der wahrscheinlichsten
Verteilungsfunktion
Ohne Frames
Maximum
Likelihood Estimation schätzt eine Verteilungsfunktion aus einer
Stichprobe. Im Gegensatz zur Kleinsten Quadrate Methode, Ordinary Least
Squares, OLS, minimiert sie nicht die restliche Streuung (unaufgeklärte
Varianz), sondern sucht diejenige Verteilungsfunktion, aus der die
vorliegende Stichprobe am wahrscheinlichsten stammt.
zurück zum Glossar (Maximum Likelihood Estimation)
Maximum Likelikood
Estimation, MLE
Sehr
verbreitete mathematische Schätzmethode, bei der man ausgehend von einer Stichprobe
die "wahre" Verteilungsfunktion der Grundgesamtheit schätzt.
Dabei
muss die Art der vorliegenden Verteilungsfunktion aus anderen
Quellen bereits bekannt sein.
MLE
schätzt diejenigen Parameterwerte der Verteilungsfunktion, für die die
Wahrscheinlichkeit, dass genau die vorliegende Stichprobe gezogen wird,
am grössten ist, also:
Bei
welchen Parameterwerten der Verteilungsfunktion wird die
Ziehungswahrscheinlichkeit für die vorliegende Stichprobe am
grössten?
Es
wird eine sogenannte Likelihood Funktion gebildet. Diese Funktion ist allgemein wie folgt
aufgebaut:
| Alle n
Messwerte der Stichprobe sind bekannt |
Von den n
Messwerten der Stichprobe sind nur die ersten m bekannt. |
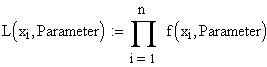 |
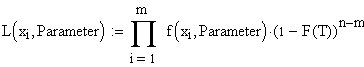 |
|
Dies ist der allgemeine
Fall.
|
Dies ist ein spezieller Fall, wie er in der Zuverlässigkeitstechnik oft vorkommt:
Man testet eine Stichprobe bis zum
Zeitpunkt T (oder bis zum xm-ten Ausfall) und bricht den
Test dann ab.
Da die letzten Datenpunkte nicht bekannt
sind, steuern sie zur Likelihood Funktion lediglich die Information
bei
"Zum Zeitpunkt T noch nicht ausgefallen".
Die entsprechende Formel für Fälle, in
denen die genauen Messwerte nicht bekannt sind und beispielsweise nur
als Intervalldaten vorliegen, wird ganz am Schluss dieser Rubrik
dargestellt.
|
|
Die Funktion stellt ein Produkt aus n Faktoren dar,
wobei n die Stichprobengrösse ist.
Je ein Faktor besteht wiederum aus der Dichtefunktion f(x) der zugrundegelegten Funktion, mit je einem aus
der Stichprobe eingesetzten x-Wert.
In die Faktoren werden also nacheinander die
Stichprobenwerte eingesetzt.
Als unbekannte Grössen sind jetzt nur noch die zu
bestimmenden Parameterwerte (typischerweise 1 oder 2) enthalten.
|
| Hier
bedeutet zusätzlch F(x) die Verteilungsfunktion. |
Gesucht
sind nun diejenigen Parameterwerte, für die diese Likelihood Funktion
maximal wird.
Dies
geschieht durch (partielles) Differenzieren nach den Parametern und =0
setzen.
Setzt
man die so ermittelten Parameterwerte in die ursprüngliche
Verteilungsfunktion ein, dann erhält man diejenige Verteilungsfunktion,
für die die Ziehungswahrscheinlichkeit der vorliegenden Stichprobe
maximal wird.
Dies
war ja das Ziel der Berechnung.
Es
sei hier nochmal erwähnt, dass die Annahme über eine bestimmte
Verteilungsfunktionsart von vorne herein gemacht werden muss. Es kann
also durchaus sein, dass die durch die MLE ermittelte "optimale"
Verteilungsfunktion immer noch "signifikant daneben" liegt, was man
durch Anpassungstests herausbekommen kann.
Mit
einfachen Worten kann man also sagen:
MLE
ermittelt unter der gegebenen Annahme (Auswahl des
Verteilungsfunktionstyps) die bestangepasste Verteilungsfunktion,
während der Anpassungstest überprüft, ob die Daten auch wirklich von
dem gewählten Verteilungsfunktionstyp sind.
Aus
rechentechnischen Gründen logarithmiert man in vielen Fällen die
Likelihood Funktion, sodass aus dem Produkt eine Summe wird: Log Likelihood Funktion. Dies ist zulässig, da die
Logarithmusfunktion monoton und stetig ist, sich also auf die
anschliessende Differenzierung nach den Parametern "nicht auswirkt".
Beispiele:
1.
Binomialverteilung.
Die
Dichtefunktion der
Binomialverteilung lautet:
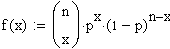
Man
hat eine Stichprobe des Umfanges n aus einer binomialverteilten
Grundgesamtheit gezogen.
Aus
der Stichprobe soll nun der "optimale" Parameter p ermittelt werden.
Mit
diesem Schritt unterstellt man bereits, dass die Grundgesamtheit
tatsächlich binomialverteilt ist und sucht "nur noch" nach der hierfür
am Besten passenden Wahrscheinlichkeit p.
Die
Likelihood Funktion lautet hier:
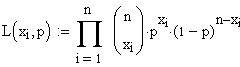 wohlgemerkt: p ist die gesuchte Variable.
wohlgemerkt: p ist die gesuchte Variable.
Hier
ergeben sich zunächst 2 wesentliche Erleichterungen:
1.
Da die Vorfaktoren 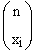 zusammen eine vom
zu ermittelnden Parameter p unabhängige Konstante bilden, kann man sie
für die folgende Rechnung weglassen.
zusammen eine vom
zu ermittelnden Parameter p unabhängige Konstante bilden, kann man sie
für die folgende Rechnung weglassen.
2.
Die Menge xi besteht nur aus einem einzigen Wert, nämlich
der "Anzahl Erfolge".
Die
Likelihood Funktion lässt sich also auf folgende Form reduzieren:
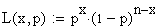
Aus
rechentechnischen Gründen logarithmiert man diese Funktion:
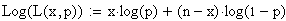
Differenzierung nach p ergibt:
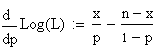
Setzt
man diesen Ausdruck =0 und löst nach p auf, so erhält man (fast
erwartungsgemäss):
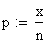
2.
Poissonverteilung
Die
Dichtefunktion
der Poissonverteilung lautet:
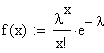
Man
hat eine Stichprobe des Umfanges n aus einer poissonverteilten
Grundgesamtheit gezogen.
Aus
der Stichprobe soll nun der "optimale" Parameter Lambda ermittelt
werden.
Mit
diesem Schritt unterstellt man bereits, dass die Grundgesamtheit
tatsächlich poissonverteilt ist und sucht "nur noch" nach dem hierfür
am Besten passenden Mittelwert Lambda.
Die
Likelihood Funktion lautet hier:
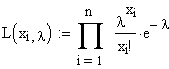
Nach
Umformung und Zusammenfassung ähnlicher Terme ergibt sich:
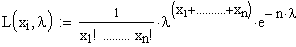 =
= 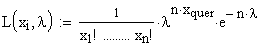
Auch
hier logarithmiert man wieder aus rechentechnischen Gründen und erhält:
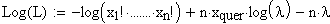
Differenzierung nach l ergibt:
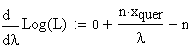
Setzt
man diesen Ausdruck =0 und löst nach l auf,
so erhält man (fast erwartungsgemäss):
xquer
= l
3. Normalverteilung
Die
Durchführung der Maximum Likelihood Estimation ist hier etwas
rechenintensiver.
Die
Dichtefunktion der
Normalverteilung lautet:
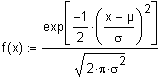
Die
Likelihood Funktion lautet hier:
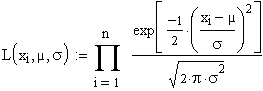
Nach
Umformung und Zusammenfassung ähnlicher Terme ergibt sich:
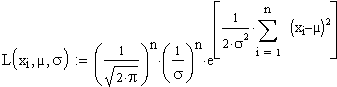
Auch
hier logarithmiert man wieder aus rechentechnischen Gründen und erhält:
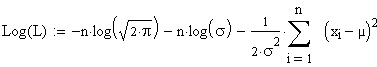
| Differenzieren
nach µ ergibt |
Differenzieren
nach Sigma ergibt |
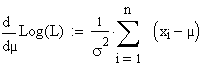 |
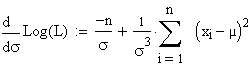 |
| Nullsetzen und Umformung nach µ bzw. Sigma ergibt
(fast erwartungsgemäss) |
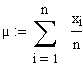 |
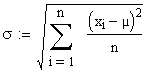 |
Da
die Normalverteilung 2 Parameter hat, ist Folgendes zu beachten:
Der
gemeinsame Vertrauensbereich der beiden Parameter (µ und s) ist nicht gleich den
Vertrauensbereichen der beiden einzelnen Parameter.
Mittels
geeigneter Statistiksoftware bekommt man den gemeinsamen
Vertrauensbereich als "Vertrauensellipse" im zweidimensionalen Raum,
bestehend aus den Achsen µ und s,
dargestellt.
Dieser
Sachverhalt wird in der Rubrik Multiple
lineare Regression beispielhaft berechnet.
4.
Exponentialverteilung
Die
Dichtefunktion
der Exponentialverteilung lautet:
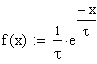 , bzw.
, bzw. 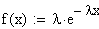
mit
l = 1/t, l: Ausfallrate und tau: MTBF.
Die
Likelihoodfunktion lautet:
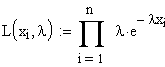 .
.
Umgeformt
ergibt dies: 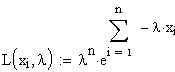
Durch
Logarithmieren erhält man die Log Likelihood Funktion:
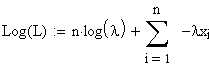 .
.
Differenzieren
nach l ergibt
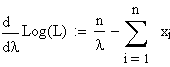
Nullsetzen
und Auflösen nach l ergibt
schliesslich
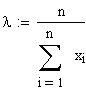 . Entsprechend würde man erhalten:
. Entsprechend würde man erhalten: 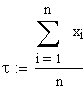
In
die Zuverlässigkeitstechnik übertragen bedeutet das:
Der
Schätzwert für die mittlere Lebensdauer t ist die kumulierte
Laufzeit geteilt durch die Anzahl festgestellter Ausfälle.
Dabei
wurde jede ausgefallene Einheit sofort
wieder ersetzt.
Werden
ausgefallene Einheiten nicht ersetzt, und wird der Test
abgebrochen, bevor alle Einheiten ausgefallen sind, dann sehen die
Formeln etwas anders aus.
Ausgehend
von der in der einleitenden Tabelle rechts angegebenen Formel erhält
man für die Likelihood Funktion:
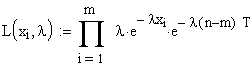 |
Hier
bedeutet T der Zeitpunkt, an dem der Test abgebrochen wurde. |
| Durch
Umformen, logarithmieren, nach l ableiten
und Nullsetzen erhält man schliesslich: |
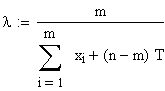 |
5.
Intervalldaten
Schliesslich
sei noch kurz der Fall erwähnt, dass die Daten nicht exakt vorliegen,
sondern nur in Form von Intervallen.
Dies
ist der Fall, wenn nur nach gewissen Zeitabständen nachgesehen werden
kann wieviele Teile seit dem letzten Nachsehen ausgefallen sind.
Zusätzlich
sei der Test zum Zeitpunkt T abgebrochen worden,
Die
Likelihood Funktion lautet dann:
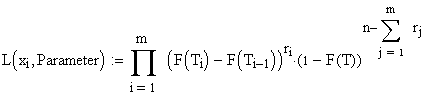 |
|
Hier bedeuten
Ti
: Zeitpunkte, zu denen nachgesehen wird,
T: Zeitpunkt, an
dem Ter Test abgebrochen worden ist,
m: Häufigkeit des
Nachsehens.
rj, rj:
Zahl der Ausfälle seit dem vorhergehenden Nachsehen.
F:
Verteilungsfunktion (Integral der Dichtefunktion)
|
Siehe
auch Likelihood Ratio Test.
zurück zum Glossar (Maximum Likelihood Estimation)
27.08.2005
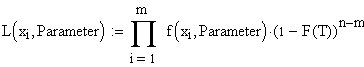
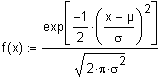
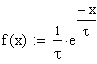 , bzw.
, bzw. 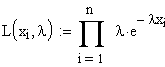 .
. 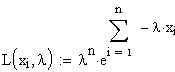
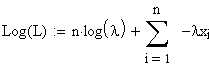 .
. 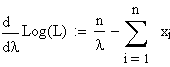
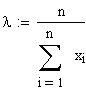 . Entsprechend würde man erhalten:
. Entsprechend würde man erhalten: