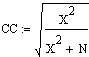 N: Anzahl Einzelwerte. CC=
[0....<1], X2: Chi Quadrat Verteilung
N: Anzahl Einzelwerte. CC=
[0....<1], X2: Chi Quadrat VerteilungAOQ, Average Outgoing Quality
Siehe Durchschlupf
19.08.2005
Siehe DoE, Begriffserklärungen.
13.10.2005
Siehe Post Hoc Test.
19.08.2005
Gegenteil der a priori Vorgehensweise. Siehe auch Post Hoc Test.
Bei umfangreichem Datenmaterial, und/oder bei Mangel an Vorwissen die übliche Vorgehensweise (--> explorative Datenanalyse).
Zuerst wird das Datenmaterial auf Besonderheiten abgesucht (explorative Datenanalyse).
Dann werden die gefundenen Auffälligkeiten mittels statistischer Hypothesentests auf Signifikanz untersucht.
A
posteriori bedeutet wörtlich "Im Nachhinein". Man führt also erst nach
der Datenaufbereitung statistische Tests durch.
A
posteriori Vorgehensweisen sind gegenüber a priori Vorgehensweisen
generell weniger aussagekräftig. Diese Aussage ist akademisch zu
verstehen, denn eine Konkurrenz zwischen diesen Beiden (Vorwissen
<--> kein Vorwissen) besteht nicht.
19.08.2005
"Näherungsweise".
Bei statistischen Tests begegnet man häufig der Aussage "Die Prüfgrösse ist approximativ normalverteilt".
Das bedeutet, dass die Prüfgrösse umso besser normalverteilt ist, also umso besser direkt mit der Normalverteilung erklärt werden kann, je grösser die getestete Stichprobe ist.
Siehe auch (approximative) Vertrauensintervalle.
19.08.2005
QS9000: Advanced Product Quality Planning.
Qualitätsplanungsprozess, bei dem bereits in frühester Phase versucht wird, "an alles" zu denken.
Der gesamte Produktlebenszyklus wird bereits geplant, wenn das Produkt erst auf Skizzen existiert.
Zentrales Qualitätswerkzeug ist hier die FMEA.
19.08.2005
Sammelbezeichnung für Tests, die man vor einem allgemeinen Test ( Omnibus Test, z.B.: ANOVA) durchführt.
Auch geplante Tests genannt.
A priori Tests beruhen auf linearen Kontrasten.
Für weitere Erklärungen zu A Priori Vergleichen siehe dort.
19.08.2005
Gegenteil von a posteriori Vorgehensweise.
Aufgrund von Vorwissen oder Vermutungen werden selektive statistische Tests (also keine Omnibus Tests) auf das Datenmaterial direkt angewandt.
Siehe insbesondere lineare Kontraste.
19.08.2005
Acceptable Quality Level
Derjenige Gutanteil, über den ein Los verfügen muss, damit es z.B. mit 90% Sicherheit bei dem Stichprobentest auch tatsächlich für gut befunden wird.
AQL und RQL sind 2 Punkte, mit denen die Operationscharakteristik eindeutig bestimmt ist.
Siehe Operationscharakteristik Beispiel.
19.08.2005
Arrhenius, Gleichung
Zusammenhang
zwischen der absoluten Temperatur und der erwarteten
Lebensdauer
(bzw.
Fehlerrate).
19.08.2005
AutoRegressive Integrated Moving Average Modell.
Dieses Modell dient zur Beschreibung von Datenreihen in der Zeitreihenanalyse und ist so allgemein, dass es mehrere unter anderem Namen bekannte Methoden als Spezialfälle enthält.
Ziel der aus den 3 Parametern p,d,q bestehenden Methode ARIMA(p,d,q) ist es:
Die vorliegende Messreihe vollständig zu beschreiben
zukünftige Werte der Zeitreihe vorherzusagen.
19.08.2005
Siehe ARIMA.
19.08.2005
Zusammenhangsmass, basierend auf der Chi Quadrat Verteilung.
Drückt den Grad von Zusammenhängen in Kontingenztafeln aus.
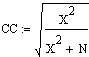 N: Anzahl Einzelwerte. CC=
[0....<1], X2: Chi Quadrat Verteilung
N: Anzahl Einzelwerte. CC=
[0....<1], X2: Chi Quadrat Verteilung
Siehe Kontingenzkoeffizient und Tabelle Korrelationskoeffizienten.
19.08.2005
Accelerated Stress Test.
Beschleunigter Test zur schnellen Aufdeckung von Schwachstellen in Produkten.
Siehe ALT.
19.08.2005
In statistischem Kontext = approximativ.
30.072006
Asymptotischer Test
Asymptotische Tests basieren auf bestimmten Verteilungsfunktionen, sind also umso besser, je grösser die Stichproben sind.
Siehe auch exakter Test.
19.08.2005
"Gegenteil"
des messbaren Merkmals. Man kann es nicht messen, sondern muss es mit Worten oder Bildern beschreiben.
19.08.2005
Das Versagen eines Individuums in einer Weise, dass der geplante Zweck nicht mehr gewährleistet ist.
19.08.2005
In der Zuverlässigkeitstechnik auf 1 normierter Anteil der Population, die zum Betrachtungszeitpunkt nicht mehr funktionsfähig ist, F(t).
Ausfallfunktion + Bestandsfunktion = F(t) + R(t) = 1
Entspricht in der allgemeinen Statistik einer Verteilungsfunktion.
Kann verbal z.B. wie folgt ausgedrückt werden:
"Nach einem Jahr sind 20% aller Geräte bereits ausgefallen".
Die mit -1 multiplizierte Ableitung der Bestandsfunktion R(t) ist die Ausfall dichtefunktion.
19.08.2005
Mit
-1 multiplizierte zeitliche Ableitung der
Bestandsfunktion R(t): -d/dt[R(t)]
Entspricht in der allgemeinen Statistik einer Dichtefunktion.
Derjenige Anteil der (noch funktionierenden) Population, der pro Zeiteinheit zum Betrachtungszeitpunkt ausfällt.
Kann verbal z.B. wie folgt ausgedrückt werden:
"Zur
Zeit fallen pro Jahr 20% aus, bezogen auf die ANFÄNGLICHE
Gesamtpopulation."
Zur Abgrenzung dieses Satzes siehe weiter unten unter Ausfallrate.
Siehe auch Ausfallratenfunktion.
19.08.2005
Spezialfall konstante Ausfallrate (wenn die Bestandsfunktion eine Exponentialverteilung ist):
Kann verbal z.B. wie folgt ausgedrückt werden:
"Zur Zeit fallen pro Jahr 20% aus, bezogen auf den noch nicht ausgefallenen Teil der Population."
Zur Abgrenzung dieses Satzes siehe weiter oben unter Ausfalldichtefunktion.
Die Ausfallrate ist normalerweise eine von der Zeit unabhängige Konstante.
Bei Zeitabhängigkeit wird der Begriff Ausfallratenfunktion verwendet. Siehe eins weiter unten.
Die generelle Funktionsweise von MTBF Berechnungen wird hier beschrieben.
Tests, die speziell auf sich ändernde Ausfallraten testen, befinden sich hier.
19.08.2005
Lambda(t), auch Hazard Rate, h(t) genannt.
Quotient aus Ausfalldichtefunktion und [1- Ausfallfunktion], also der auf den gegenwärtigen Bestand bezogene Anteil der Population, der pro Zeiteinheit ausfällt. Allgemein statistisch formuliert: Quotient aus Dichtefunktion und [1- Verteilungsfunktion]:
Bei F(t) = Exponentialverteilung nimmt die Ausfallratenfunktion einen konstanten Wert an, die Ausfallrate.
Kann verbal z.B. wie folgt ausgedrückt werden:
"Zur
Zeit fallen pro Stunde 5% aus, bezogen auf den noch nicht ausgefallenen Teil der Population."
Der Begriff Ausfallratenfunktion wird im Gegensatz zur Ausfallrate dann verwendet, wenn diese von der Zeit abhängt.
19.08.2005
Sammelbegriff zur Ermittlung der optimalen Parameter eines (statistischen oder mathematischen) Modells mit dem Ziel der besten Anpassung an gegebene Daten.
14.11.2005
Die Gesamtheit aller möglichen Werte einer Variablen oder eines Merkmals.
Oft auch als Bezeichnung für den jeweils gerade vorliegenden Wert verwendet.
Beispiel Würfeln:
Die Variable "Augenzahl" kann die Ausprägungen 1,2,3,4,5 und 6 annehmen.
Wurde eine 6 gewürfelt, dann hatte die Variable zuletzt die Ausprägung 6.
19.08.2005
Messwert,
der sich von den anderen Messwerten deutlich unterscheidet. Es gibt
keine allgemein anerkannte Definition. Meistens handelt es sich
schlicht um unliebsame Messwerte.
19.08.2005
= n/N, wobei N die Grösse der
Grundgesamtheit und n die
Grösse der
Stichprobe
ist. Eine relative Stichprobengrössenangabe.
27.11.2005
Faltung einer Wertereihe.
19.08.2005
Grundlegende, nicht beweisbare, aber sinnvolle, und im Geltungsbereich der darauf aufbauenden Theorie unhinterfragte Aussage.
13.09.2005