Ausfallabstand
Relevante Fälle
Anzahl
Signifikanztabelle, H0:
Verbesserungstrend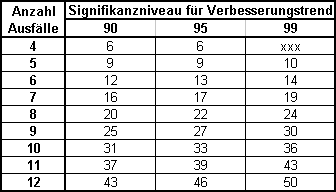
20
40
70
60
60
80
5
40
70
60
60
80
4
20
70
60
60
80
4
70
80
1
10
60
60
80
3
60
80
1
60
80
1
80
xxx
Summe
19
zurück zum Glossar (Reverse Arrangement Test)
Im Folgenden werden 3 Signifikanztests beschrieben, die speziell auf zuverlässigkeitstechnische Belange zugeschnitten sind.
Diese
Tests sind natürlich nicht auf die Zuverlässigkeitstechnik beschränkt,
sie finden hier aber
die meisste Anwendung.
Reverse Arrangement Test (keine Annahmen über die Verteilungsart)
Mil-Handbuch Test (Annahme: Duane Modell, d.h.: Ausfallrate ~ Potenzfunktion)
Laplace Test (Annahme: Ausfallrate ~ Exponentialfunktion)
Bei allen Tests ist die Nullhypothese einseitig formuliert und lautet
H0: "Die zeitlichen Abstände zwischen benachbarten Ausfällen nehmen zu (ab) = Die Ausfallrate nimmt ab (zu)"
Dieser Test enthält keinerlei Annahmen über die mathematische Beschaffenheit des hinter den Daten vermuteten Verbesserungs- (oder Verschlechterungs-) modells (parameterfreier Test).
Dieser Test ist ein allgemeiner Test auf Trend und nicht auf die Zuverlässigkeitstechnik beschränkt.
Er basiert auf dem Abzählen von Fehlordnungen.
Fehlordnungen sind "lokal beschränkte Gegentrends", die einem postulierten "globalen Trend" entgegenstehen.
Vorgehensweise anhand eines Beispiels
1. Ausfallzeitpunkte in eine chronologische Reihe schreiben
|
Ausfallzeitpunkte |
||||||||
|
20 |
60 |
80 |
150 |
160 |
220 |
280 |
360 |
Testabbruch bei 400 |
Nullhypothese: "Die Abstände zwischen den Ausfallzeitpunkten nehmen zu, d.h.: Die Fehlerrate wird geringer".
Da wir einen Verschlechterungstrend explizit ausschliessen, haben wir die Hypothese einseitig formuliert.
2. Die Differenzen zwischen den Ausfallzeitpunkten in eine chronologische Reihe schreiben
|
Ausfallzeitpunkte bzw. Zeitdauern zwischen 2 Ausfällen |
Testabbruch (kein Ausfall) |
|||||||
|
20 |
60 |
80 |
150 |
160 |
220 |
280 |
360 |
400 |
|
20 |
40 |
20 |
70 |
10 |
60 |
60 |
80 |
(40) |
3. Ermitteln der Anzahl der "relevanten Fälle". Dies ist die Prüfgrösse. Fehlordnungen sind Nicht-relevante Fälle.
Man betrachtet den ersten Ausfallabstand (=20) und zählt nach, wie oft dieser Ausfallabstand zu späteren Zeiten überschritten worden ist: 40,70, 60, 60, 80, also 5 Fälle. Für den zweiten Ausfallabstand (=40) ergibt sich 70, 60, 60, 80, also 4 Fälle. So verfährt man mit allen Ausfallabständen.
Bei einer Reihe mit stetig zunehmenden Ausfallabständen sowie der Bedingung "Testabbruch ohne Ausfall" würde man maximal n(n-1)/2 relevante Fälle erhalten.
n ist die Anzahl Ausfallabstände.
Insgesamt ergibt sich in diesem Beispiel:
|
Ausfallabstand |
Relevante Fälle |
Anzahl |
Signifikanztabelle, H0:
Verbesserungstrend |
||||
|
20 |
40 |
70 |
60 |
60 |
80 |
5 |
|
|
40 |
70 |
60 |
60 |
80 |
|
4 |
|
|
20 |
70 |
60 |
60 |
80 |
|
4 |
|
|
70 |
80 |
|
|
|
|
1 |
|
|
10 |
60 |
60 |
80 |
|
|
3 |
|
|
60 |
80 |
|
|
|
|
1 |
|
|
60 |
80 |
|
|
|
|
1 |
|
|
80 |
xxx |
|
|
|
|
|
|
|
Summe |
19 |
||||||
4. Prüfen, ob das Ergebnis signifikant ist.
Im Beispiel sind 8 Ausfallabstände. Die maximal denkbare Anzahl relevanter Fälle r liegt also bei r = 8*7/2 =28. Als Durchschnitt würde man die Hälfte, 14 erwarten. Tatsächlich liegen 19 relavante Fälle vor.
Aus der Signifikanztabelle ist zu entnehmen, dass für 90% statistische Sicherheit bei 8 Ausfallabständen 20 relevante Fälle erforderlich wären. Das Ergebnis ist also zum Niveau 90% nicht signifikant, die Nullhypothese kann also nicht verworfen werden.
Wenn man einseitig auf negativen Trend testen will, also die Nullhypothese lautet
H0: "Die zeitlichen Abstände zwischen benachbarten Ausfällen nehmen ab",
dann stehen in der Signifikanztabelle anstatt [Tabellenwert] nun [n(n-1)/2-Tabellenwert].
Bei n=4 Ausfällen und 90% würde also der Tabellenwert 4*3/2-6 = 0 anstelle 6 , bei n=5 und 90% 5*4/2-9 = 1 stehen, usw.
Wenn n grösser ist als 12, so kann man mit folgender Formel arbeiten.
Die Prüfgrösse ist approximativ standardnormalverteilt.
Der kritische Wert ergibt sich zu
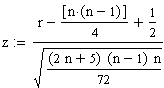
Das einseitige Signifikanzniveau für Abnahme der Ausfallrate erhält man beispielsweise mit der Excelformel [2*STANDNORMVERT(z)-1].
Für n=8 und r=20 (aus Tabelle oben) erhält man z = 1.6083, was einem Signifikanzniveau von 89.2% entspricht.
Die Formel rechnet für kleine n also konservativ (Die Formel sagt "nicht signifikant" zu 90%, während die Tabelle für 90% bereits Signifikanz signalisiert).
Möchte man gegen ansteigende Ausfallrate testen, dann muss man in der Formel r durch n(n-1)/2-r ersetzen.
zurück zum Glossar (Reverse Arrangement Test)
15.01.2006
zurück zum Glossar (Mil-Handbuch Test)
Dieser Test testet am genauesten, wenn ein Duane Zuverlässigkeitswachstumsmodell zugrundegelegt wird,
die
Ausfallrate h(t) also einem
Potenzgesetz ![]() ,
0<b<1 folgt.
,
0<b<1 folgt.
Die Nullhypothese lautet demnach:
H0: "Die zeitlichen Abstände zwischen benachbarten Ausfällen folgen einem Duane Modell"
Die Prüfgrösse ist Chi Quadrat verteilt mit 2n Freiheitsgraden.
|
|
n: Anzahl Ausfälle Ti: Zeitpunkt des i-ten Ausfalls Tabbruch: Zeit, nach der der Test ohne Ausfall abgebrochen worden ist. Das a hat nichts mit dem a in der obigen Formel für h(t) zu tun. |
Bei einem Test auf Zuverlässigkeitswachstum wählt man als Schwellwert für a typischerweise 80% oder mehr.
Testst man Zuverlässigkeitsverschlechterung, wählt man als Schwellwert für a typischerweise 20% oder weniger.
Die Berechnung von a kann beispielsweise mittels folgender Excelformel erfolgen: [1-CHIVERT(Prüfgrösse,2n)].
Für das Zahlenbeispiel aus dem Reverse Arrangement Test
|
Ausfallzeitpunkte |
Testabbruch (kein Ausfall) |
|||||||
|
20 |
60 |
80 |
150 |
160 |
220 |
280 |
360 |
400 |
erhält man für die Prüfgrösse den Wert 18.91.
1-CHIVERT(18.91,16) ergibt a = 72.7%.
Die Nullhypothese kann also nicht verworfen werden.
zurück zum Glossar (Mil-Handbuch Test)
27.08.2005
zurück zum Glossar (Laplace Test)
Laplace Test (Schwerpunkttest)
Wird vermutet, dass das Zuverlässigkeitswachstum eher einer Exponentialfunktion als einer Potenzfunktion (-> Mil-Handbuch Test) folgt, dann ist der Laplace Test besser geeignet.
Ausfallrate
gemäss
Exponentialgesetz: ![]() ,
b<0
,
b<0
Die Nullhypothese lautet demnach:
H0: "Die zeitlichen Abstände zwischen benachbarten Ausfällen folgen einem Exponentialgesetz"
Die Prüfgrösse ist standardnormalverteilt.
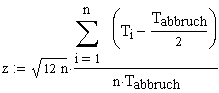 |
n: Anzahl Ausfälle Ti: Zeitspanne zwischen dem (i-1)-ten und i-ten Ausfall. Tabbruch: Zeit, nach der der Test ohne Ausfall abgebrochen worden ist.
|
Das einseitige Signifikanzniveau a für Abnahme der Ausfallrate erhält man beispielsweise mit der Excelformel STANDNORMVERT, und zwar
[1-2*STANDNORMVERT(z)], falls z < 0 (sinkende Ausfallrate)
[2*STANDNORMVERT(z)-1], falls z > 0 (steigende Ausfallrate)
Für das Zahlenbeispiel aus dem Reverse Arrangement Test
|
Ausfallzeitpunkte |
Testabbruch (kein Ausfall) |
|||||||
|
20 |
60 |
80 |
150 |
160 |
220 |
280 |
360 |
400 |
ergibt sich z = -0.827 -> (Fall 2.) a = 59.16%.
Die Nullhypothese kann also nicht verworfen werden.
zurück zum Glossar (Laplace Test)
21.08.2005
Datenschutzhinweise