Masskorrelationskoeffizient
Produkt-Moment-Korrelationskoeffizient
Bravais Pearsonscher Korrelationskoeffizient
Siehe auch diese Exceldatei für ein Zahlenbeispiel mit Gegenüberstellung von
-
Kontingenzkoeffizient Phi,
-
Spearman's r
-
Pearson'scher Korrelationskoeffizient.
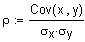Cov = Kovarianz
metrisch / metrisch
Siehe auch diese Exceldatei für ein Zahlenbeispiel mit Gegenüberstellung von
- Kontingenzkoeffizient Phi,
- Spearman's rho
- Pearson'scher Korrelationskoeffizient.
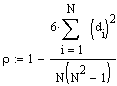
N: Gesamtanzahl Wertepaare
di: Differenz der Rangwerte des Wertepaares i
Derivat des Produkt-Moment-Korrelationskoeffizienten.
ordinal / ordinal
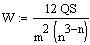Siehe hierRangkorrelations koeffizient Tau
Kendalls Tau ist mächtiger als der Spearmansche Rangkorrelationskoeffizient. Für eine genaue Beschreibung siehe hier.
Während Spearman lediglich 2 Messreihen paarweise auswertet, kann Kendalls Tau auch auf Kontingenztabellen angewendet werden.
Für die Anwendung auf Kontingenz
tabellen gedacht
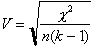
k = der kleinere Wert der Anzahl der Zeilen oder der Spalten.
n: Gesamtanzahl Werte
X2: Chi Quadrat
nominal / nominal
Siehe auch diese Exceldatei für ein Zahlenbeispiel mit Gegenüberstellung von
- Kontingenzkoeffizient Phi,
- Spearman's r
- Pearson'scher Korrelationskoeffizient.
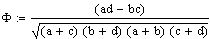
Zusammenhang mit der X2 Verteilung
(siehe Vierfeldertafel Test):
--> 
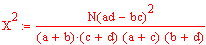
Auflösen nach X2 ergibt die Prüfgrösse für
F
F ist ein Derivat des Produkt-Moment-Korrelationskoeffizienten
Nur bei 2*2 Tabellen. (= Vier Felder Tafeln)
X2: Chi
Quadrat
(Man kann sich die beiden dichotomen Skalen als "quasimetrische" Skalen vorstellen, die lediglich aus den Werten 0 und 1 bestehen)
Anmerkungen:
Der mögliche Wertebereich von F kann deutlich kleiner sein als [-1.....+1].
Man erkennt das, wenn man eine Vierfeldertafel mit Zahlenbeispielen belegt und versucht, "extreme" Zahlenkonstellationen unter Beibehaltung der Randhäufigkeiten zu finden.
Beispiel siehe hier
Verglichen werden die Anteile richtiger Zuordnungen mit und ohne Einbeziehung von in der Tabelle verfügbarer Information.
Allgemein: (Anteil der neu hinzugekommenen
richtigen
Vorhersagen) / (Anteil der ursprünglich falschen Vorhersagen)
Beispiel siehe hier
Assoziationskoeffizient C,
Kontingenzkoeffizient C (Pearson)
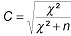
X2: Chi Quadrat
n: Gesamtanzahl Wertepaare
Anmerkung:
Manchmal wird für C auch die Formel
angegeben
(j = Anzahl Zeilen , Spalten,...wobei j die kleinste der
Zahlen sein muss)
Beschreibt einen Zusammenhang zwischen einem echt dichotomen (also nominalskalierten ) und einem normalverteilten Merkmal.
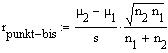
n1,n2: Stichprobenumfänge auf den beiden Stufen des dichotomen Merkmals,
s: Standardabweichung des kontinuierlichen Merkmals,
µ1,µ2: Mittelwerte des kontinuierlichen (metrischen) Merkmals auf den Stufen 1 und 2 des dichotomen Merkmals.
Derivat des Produkt-Moment-Korrelationskoeffizienten .
Signifikanztest:
Mit der unter Fisher Transformation angegebenen Formel
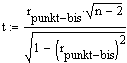
Beispiel siehe dort.
Beschreibt einen Zusammenhang von zwei metrischen und
jeweils normalverteilten Variablen. Dabei ist eine der beiden
Variablen künstlich dichotomisiert ( = in zwei Kategorien aufgeteilt) worden.
Beispiel:
Künstliche Dichotomisierung macht man bei Umfragen, wo an sich metrische Merkmale mit Ja/Nein, Gut/Schlecht bewertet werden sollen.
Der damit einhergehende Informationsverlust wird in Kauf genommen, wenn man sich beispielsweise prinzipiell für das Haushaltseinkommen in Abhängigkeit des Alters interessiert, das Ergebnis jedoch in "Rentner" und "Nicht-Rentner" aufschlüsseln und auf dieser Basis Korrelationsberechnungen anstellen will.
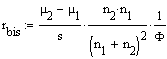
F ist die Ordinate (Wert auf der vertikalen Achse) der Standardnormalverteilung, die sie in die Anteile n1/(n2+n1) und n2/(n2+n1) aufteilt.
Beispiel:
n1=6 und n2=6 -> n1/(n2+n1) =6/(6+6) =0.5
-> Für welches z bekommt die (kumulierte) Standardnormalverteilung den Wert 0.5?
-> Excelfunktion STANDNORMINV(0.5) = 0
-> Dunktionswert der Dichtefunktion der Standardnormalverteilung an der Stelle 0.5?
-> Excelfunktion NORMVERT(0,0,1,falsch) = 0.3989
-> F =0.3989.
µ1 und µ2 sind die Mittelwerte des kontinuierlichen Merkmals auf den Stufen 1 und 2.
s ist die Standardabweichung des kontinuierlichen Merkmals.
Derivat des Produkt-Moment-Korrelationskoeffizienten
Beschreibt einen Zusammenhang von zwei metrischen und jeweils normalverteilten Variablen. Dabei sind beide Variablen künstlich dichotomisiert ( = in zwei Kategorien aufgeteilt) worden .
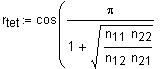
nxy = Besetzungszahlen der Vierfeldertafel.
Künstliche Dichotomisierung macht man bei Umfragen, wo an sich metrische Merkmale mit Ja/Nein, Gut/Schlecht bewertet werden sollen.
Der damit einhergehende Informationsverlust wird in Kauf genommen, wenn man sich beispielsweise prinzipiell für das Haushaltseinkommen in Abhängigkeit des Alters interessiert, das Ergebnis jedoch in "Rentner" und "Nicht-Rentner" aufschlüsseln und auf dieser Basis Korrelationsberechnungen anstellen will.
Signifikanztest:
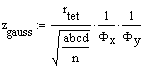
zgauss: Standardnormalverteilung
a,b,c,d: Randhäufigkeiten der Vierfeldertafel.
Fx, Fy : Berechnung siehe Beislpiel oben unter "Biseriale Korrelation"
Hier sind jedoch 2 F's zu berechnen. Bei der Berechnung des 2. F denkt man sich das Koordinatensystem einfach um 90 Grad gedreht.
Für n1 und n2 sind die jeweiligen Randhäufigkeiten zu nehmen.
Beschreibt einen Zusammenhang zwischen einem echt dichotomen (also nominalskalierten ) und einem weiteren Merkmal auf ordinalem Niveau.
Die Vorgehensweise entspricht derjenigen des Mann-Whitney Tests.
Die Stufen der dichotomen Skala werden als Gruppen aufgefasst.
Für beide Gruppen werden wie im Mann Whithey Test die Rangsummen und daraufhin die folgenden Werte berechnet:
-->
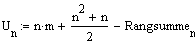
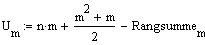
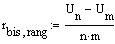
n+m: Gesamtanzahl Wertepaare
n,m: Anzahl Wertepaare auf der 1. bzw. 2. Stufe des dichotomen Merkmals.
Signifikanz wird genauso wie beim Mann-Whitney Test überprüft.
Dabei wird das Datenmaterial wieder als 2 Stichproben, repräsentiert durch das dichotome Merkmal, aufgefasst.
Korrelation zweier Variablen, nachdem der Einfluss weiterer Variablen herausgerechnet (herauspartialisiert) worden ist.
Alle "Nonsenskorrelationen" (Beispiele siehe Kausalität) entstehen dadurch, dass man vergessen hat, mindestens eine dritte, "vermittelnde Variable" herauszurechnen.
Es existiert keine Berechnungsformel.
--> Näherungsweise mit Partieller Korrelation arbeiten.