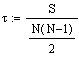hier in diesem Beispiel: = -0,4. zurück zum Glossar (Kendalls Tau)
Ein Rangkorrelationskoeffizient (-1.....+1). Weniger verbreitet als der Spearmansche Rangkorrelationskoeffizient, jedoch weitaus mächtiger.
Im Gegensatz zu anderen Korrelationskoeffizienten werden ALLE Wertepaare UNTEREINANDER verglichen, nicht nur je die 2 Werte eines Paars.
Ausserdem ist die Anwendung von Kendalls Tau nicht auf Wertepaar-Reihen beschränkt, sondern kann auf beliebig grosse K x L Kontingenztafeln angewendet werden (Anmerkungen hierzu ganz unten)
Es gibt 3 "Varaianten" von Kendalls Tau. Siehe hierzu am Ende dieser Rubrik.
Im Gegensatz zum Spearmanschen Rangkorrelationskoeffizienten wird anstatt der quadrierten Rangdifferenzen die Fehlordnung der Paare untereinander ausgewertet.
Deswegen ist Kendalls Tau unempfindlicher gegenüber Ausreissern.
Beispiel 1, ohne Ties
1.)
Ordnen einer der beiden zusammenhängenden Rangreihen nach Rangnummer, wobei die Paare erhalten bleiben.
Rangreihe 2 nimmt also zwangsläufig in der Regel irgendeine "fehlgeordnete" Form an.
| Rangreihe_1 | 1 | 2 | 3 | 4 | 5 |
| Rangreihe_2 | 3 | 1 | 2 | 5 | 4 |
2.)
Bildung aller denkbaren Rangpaare der "fehlgeordneten" Rangreihe.
Mit 5 Werten ergeben sich also 4+3+2+1 = 5*(5-1)/2 = 10 Paare.
(Allgemein: N(N-1)/2)
| 3-1 | 3-2 | 3-5 | 3-4 | 1-2 | 1-5 | 1-4 | 2-5 | 2-4 | 5-4 |
3.)
Unterscheidung, ob der jeweils erste Wert der Paare
kleiner (Proversion [P],"+") oder
grösser (Inversion [I],"-")
als der jeweils zweite Wert ist.
| 3-1 | 3-2 | 3-5 | 3-4 | 1-2 | 1-5 | 1-4 | 2-5 | 2-4 | 5-4 |
| - | - | + |
+ | - | - | - | - | - | + |
Es ergibt sich P=7, I=3
S = P-I = 3-7 = -4
4.)
Berechnung von Kendalls Tau
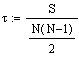hier in diesem Beispiel: = -0,4.
Dies ist Kendalls ta , auch unter dem Namen Goodman's und Kruskal's Gamma bekannt.
Signifikanztest:
a) Für N<40 (exakter Test) gibt es einschlägige Tabellen.
b) N>40:
Kendalls Tau ist bei Gültigkeit der Nullhypothese ("Die Wertereihen korrelieren miteinander") asymptotisch standardnormalverteilt mit
| Erwartungswert | 0 |
| Standardabweichung |  |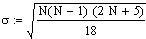
Das
standardisierte t ist Prüfgrösse
und berechnet sich zu t/
Mit
der Excelfunktion STANDNORMVERT(t/
Beispiel 2, mit Ties in nur einer Reihe.
1.)
Ordnen einer der beiden zusammenhängenden Rangreihen nach Rangnummer, wobei die Paare erhalten bleiben. Rangreihe 2 nimmt also zwangsläufig in der Regel irgendeine "fehlgeordnete" Form an.
Reihe 2 sei die Reihe mit Ties
| Rangreihe_1 | 1 | 2 | 3 | 4 | 5 |
| Rangreihe_2 | 3 | 1 | 3 | 3 | 5 |
2.)
Bildung aller denkbaren Rangpaare der "fehlgeordneten" Rangreihe.
Mit 5 Werten ergeben sich also 5*(5-1)/2 = 10 Paare.
(Allgemein: N(N-1)/2)
| 3-1 | 3-3 | 3-3 | 3-5 | 1-3 | 1-3 | 1-5 | 3-3 | 3-5 | 3-5 |
3.)
Unterscheidung, ob der jeweils erste Wert der Paare
kleiner (Proversion [P],"+"), oder
grösser (Inversion [I],"-"), oder
gleich (Tie [T],"0")
als der jeweils zweite Wert ist.
| 3-1 | 3-3 | 3-3 | 3-5 | 1-3 | 1-3 | 1-5 | 3-3 | 3-5 | 3-5 |
| - | 0 | 0 | + | + | + | + | 0 | + | + |
Es ergibt sich P=6, I=1, T=3
S = P-I = 6-1 = 5 N(N-1)/2 = P+I+T
4.)
Berechnung von Kendalls Tau
,
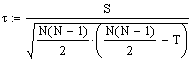wobei 
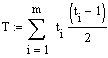
Dies ist Kendalls tb für den Fall Ties in nur einer Reihe.
Anmerkung:
Durch einfaches Umformen kommt man auf folgende Darstellung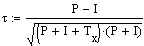 
ti:Länge des i-ten Ties (Eine Rangbindung [Tie] kann ja aus mehr als 2 Werten bestehen)
m: Anzahl aller Ties.
In
diesem Beispiel berechnet sich T
zu: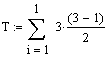 
= 3
(Es gibt nur eine einzige Rangbindung ; diese hat die Länge 3 [Weil eine Zahl {3} genau 3 mal vorkommt])
τ ergibt sich hiermit zu 0,6
Signifikanztest: Siehe Beispiel 3
Beispiel 3, mit Ties in beiden Reihen.
1.)
Ordnen einer der beiden zusammenhängenden Rangreihen (X) nach Rangnummer, wobei die Paare erhalten bleiben. Rangreihe Y nimmt also zwangsläufig in der Regel irgendeine "fehlgeordnete" Form an.
| Rangreihe_X | 1.5 | 1.5 | 3 | 4.5 | 4.5 | 6 |
| Rangreihe_Y | 1.5 | 1.5 | 4 | 3 | 6 | 5 |
Paare, die wenigstens in einer Rangreihe an Ties beteiligt sind, sind gelb hervorgehoben.
2.)
Bildung aller denkbaren Rangpaare der "fehlgeordneten" Rangreihe.
Mit 6 Werten ergeben sich also 6*(6-1)/2 = 15 Paare.
(Allgemein: N(N-1)/2)
| 1.5-1.5 | 1.5-4 | 1.5-3 | 1.5-6 | 1.5-5 | 1.5-4 | 1.5-3 | 1.5-6 | 1.5-5 | 4-3 | 4-6 | 4-5 | 3-6 | 3-5 | 6-5 |
3.)
Unterscheidung, ob der jeweils erste Wert der Paare
kleiner (Proversion [P],"+"), oder
grösser (Inversion [I],"-"), oder
gleich (Tie [T],"0")
als der jeweils zweite Wert ist.
| 1.5-1.5 | 1.5-4 | 1.5-3 | 1.5-6 | 1.5-5 | 1.5-4 | 1.5-3 | 1.5-6 | 1.5-5 | 4-3 | 4-6 | 4-5 | 3-6 | 3-5 | 6-5 |
| 0 | + | + | + | + | + | + | + | + | - | + | + | + | 0 | - |
Die rechte Null kommt deshalb zustande, weil die Werte 3 und 6 der zweiten Rangreihe aufgrund der Rangbindung 4.5-4.5 in der ersten Rangreihe prinzipiell vertauschbar sind.
Es ergibt sich P=11, I=2
S = P-I = 11-2 = 9
4.)
Berechnung von Kendalls Tau
,
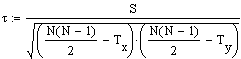wobei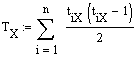 
und
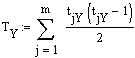
Dies ist Kendalls tb für den Fall Ties in beiden Reihen.
Anmerkung:
Durch einfaches Umformen kommt man auf folgende Darstellung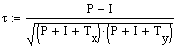
N(N+1)/2 = P + I + TX + TY - TXY
TX, TY: Ties in den Rangreihen X und Y,
TXY: Gemeinsame Ties der beiden Rangreihen X und Y (Hier nur 1, repräsentiert durch die vier 1.5 Werte)
n,m: Anzahl Rangbindungen in den Rangreihen X und Y,
tiX, tjY: Länge der jeweiligen Rangbindungen in den Rangreihen X und Y.
In diesem Beispiel ergibt sich:
N =6
TX = 2*(2-1)/2 + 2*(2-1)/2 = 2
TY = 2*(2-1)/2 = 1
TXY = 1 (In dieser Formel leider nicht berücksichtigt)
P = 9
I = 2
S=P-I =7
t ergibt sich hiermit zu 0,5189
Signifikanztest:
a) Für N<10 (exakter Test) gibt es einschlägige Tabellen.
b) N>10:
Kendalls Tau ist bei Gültigkeit der Nullhypothese ("Die Wertereihen korrelieren miteinander") asymptotisch standardnormalverteilt mit
| Erwartungswert | 0 |
| Standardabweichung |  |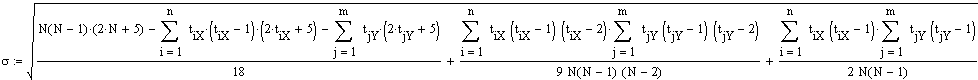
Das
standardisierte t ist Prüfgrösse
und berechnet sich zu t/
Mit
der Excelfunktion STANDNORMVERT(t/
Anmerkungen
1.
In den vorangegangenen Beispielen sind im Wesentlichen 2 grundsätzlich verschiedene Versionen von Kendalls Tau aufgetaucht:
Kendalls
τa :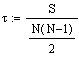
(Beispiel 1)
Kendalls
τb :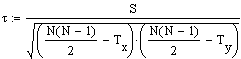
(Beispiele 2 und 3)
Kendalls
τc :
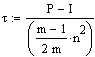(Kein
Beispiel)
m: Minimum aus [Zeilenzahl, Spaltenzahl]
2.
Wie am Anfang dieser Rubrik bereits erwähnt, ist Kendalls Tau auch auf K x L Kontingenztafeln anwendbar.
K x L Kontingenztabellen sind zweidimensional, das heisst, auch hier hat man es mit Wertepaaren zu tun.
Allerdings müssen die beiden Dimensionen ordinaler Natur sein, denn Kendalls Tau "erwartet" das Vorhandensein einer <grösser - kleiner> Relation.
Nun denkt man sich alle Wertepaare in einer Reihe aufgereiht und ordnet eine der beiden Reihen; die andere Reihe ergibt dann die fehlgeordnete Reihe.
Auf das so erhaltene Wertereihenpaar wendet man schliesslich eine Version von Kendalls Tau an.
Kendalls τb
kann auch auf Kontingenztabellen angewandt werden, jedoch nur auf quadratische.
Bei nicht-quadratischen Tabellen können die Extremalwerte -1 und +1 nicht erreicht werden.
Das liegt daran, dass der Werteumfang der beiden aus der Tabelle gewonnenen Wertereihen unterschiedlich ist.
Kendalls τc
kann auf beliebige 2-dimensionale Kontingenztabellen angewandt werden.
zurück zum Glossar (Kendalls Tau)
30.04.2015