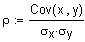zurück zum Glossar (Spearman's Rho)

Wie berechnet sich der Spearman'sche Rangkorrelationskoeffizient aus dem Produkt-Moment Korrelationskoeffizienten ?

Man geht vom Produkt-Moment Korrelationskoeffizienten aus

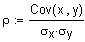  (Cov = Kovarianz), 

welcher auch wie folgt geschrieben werden kann , x_quer und y_quer: Erwartungswerte.

Mit ausmultipliziertem Zähler ergibt das    (1)

Beim Spearman'schen Rangkorrelationskoeffizienten muss man sich vor Augen halten, dass sowohl die x_i als auch die y_i vollständige, aus ganzen positiven Zahlen bestehende Reihen sind, also z.B.für n=9: 1,2,3,4,5,6,7,8,9.

In der Rubrik Ordnungsstatistik findet man für solche Zahlenreihen folgende Kenngrössen:

Mittelwert (Erwartungswert)	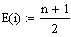-->    xquer = yquer = (n+1)/2     (2)
Varianz	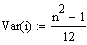-->   ,       (3)
Summe	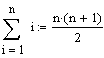-->   ,       (4)
Quadratesumme	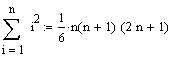-->    ,        (5)

Als ersten Schritt löst man die  binomnische Beziehung nach S2x_iy_i auf und setzt dies in (1) ein.

In die sich nun ergebende Gleichung setzt man schliesslich (2), (3),  (4) und (5) ein, kürzt alles Mögliche heraus und erhält schliesslich:

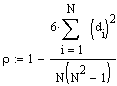
zurück zum Glossar (Spearman's Rho)

19.09.2005

 Datenschutzhinweise