Berechnet den y-Achsenabschnitt der Regressionsgeraden beim x-Wert Null, also den Wert b der Geradengleichung Y =mX + b. Beispiel: X
Berechnet die (kumulierte) Verteilungsfunktion der Betaverteilung.
Falls die beiden Parameter "obere" und "untere Grenze" weggelassen werden, übernimmt Excel die Werte 0 und 1. Beispiel: X
Berechnet die Stelle z auf der horizontalen Achse, die dem kumulierten Flächenanteil der Betaverteilung entspricht. Beispiel: X
Ziehung von genau n Elementen aus einer (unendlich grossen) binomialverteilten Grundgesamtheit mit bekanntem Anteil Merkmalsträgern. BINOMVERT berechnet die Wahrscheinlichkeit, dass unter den n gezogenen Elementen
- genau x Merkmalsträger sind (kumuliert = falsch)
- höchstens x Merkmalsträger sind (kumuliert = wahr)
Berechnet das Alpha Risiko einer Chi Quadrat verteilten Zufallsgrösse. Umkehrfunktion von CHIINV.

Beispiele: X und hier
Berechnet die Prüfgrösse des Vertrauensbereiches einer Chi Quadrat verteilten Zufallsgrösse. Umkehrfunktion von CHIVERT. Beispiele: X und hier
CHITEST berechnet das Signifikanzniveau dafür, dass die Werte einer Wertereihe (z.B. Häufigkeitsverteilungen) mit den erwarteten Werten übereinstimmen..
Hier wird also jeder Einzelwert der einen Reihe mit dem korrespondierenden Wert der zweiten reihe verglichen. Beispiele: X und hier
FTEST berechnet das Signifikanzniveau dafür, dass die Varianzen zweier Stichproben gleich sind. Beispiele: X und hier
Berechnet das Alpha Risiko einer F- verteilten Zufallsgrösse. Umkehrfunktion von FINV.
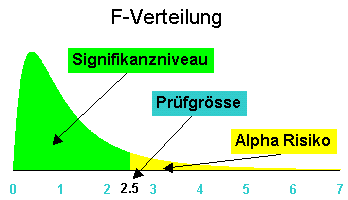
Beispiele: X und hier
Berechnet die Prüfgrösse des Vertrauensbereiches einer F- verteilten Zufallsgrösse. Umkehrfunktion von FVERT.
Berechnet die Fisher Transformierte zum Wert x. Beispiel: hier
Berechnet den ursprünglichen Wert x der Fisher Transformierten z. Beispiel: hier
Berechnet die
- Dichtefunktion der Gammaverteilung an der Stelle x (kumuliert = falsch)
- (kumulierte) Verteilungsfunktion der Gammaverteilung bis zur Stelle x.
Umkehrfunktion von GAMMAINV. Beispiel: X
Berechnet die Stelle x auf der horizontalen Achse, die dem kumulierten Flächenanteil der Gammaverteilung entspricht.
Umkehrfunktion von GAMMAVERT. Beispiel: X
Berechnet den natürlichen Logarithmus der Gammafunktion an der Stelle x.
Berechnet das geometrische Mittel einer aus maximal 30 Werten bestehenden Wertereihe
Entspricht Winsorisieren. Beispiel: Prozent = 0.2--> links und rechts werden jeweils 10%der Werte nicht beachtet.
Berechnet die relative Lage eines Wertes x im Vergleich zu einer als normalverteilt angenommenen Wertereihe. GTEST(...) = 1,5 bedeutet z.B, dass x das 1,5-fache einer Standardabweichung vom Mittelwert der Wertereihe entfernt liegt.
Der Parameter Standardabweichung ist optional, bei Weglasssen wird er aus der Wertereihe berechnet.
Berechnet das harmonische Mittel einer aus maximal 30 Werten bestehenden Wertereihe.
Ziehung von genau n Elementen aus einer (endlich grossen, hypergeometrisch verteilten) Grundgesamtheit mit bekannter Anzahl Merkmalsträger.
HYPERGEOMVERT berechnet die Wahrscheinlichkeit, dass unter den n gezogenen Elementen genau x Merkmalsträger sind. Beispiel: hier
Ziehen ohne Zurücklegen. Berechnet die Anzahl Kombinationen. Formel siehe Kombinatorik unter "Kombinationen".
Ziehung einer Stichprobe aus einer normalverteilten Grundgesamtheit mit bekannter Standardabweichung.
KONFIDENZ berechnet die halbe Breite des Vertrauensbereiches des arithmetischen Mittelwertes der Stichprobe. Beispiel: X
= PEARSON(...). Beispiel: X
Berechnet die Kovarianz einer Reihe von Wertepaaren. Beispiel: X
Ziehung von genau n Elementen aus einer aus einer unendlich grossen Grundgesamtheit mit bekanntem Anteil Merkmalsträgern.
KRITBINOM berechnet die maximale Anzahl Merkmalsträger, die mit der gegebenen Grenzwahrscheinlichkeit in diesen n Elementen enthalten sind. Die Grenzwahrscheinlichkeit entspricht mathematisch gesehen dem Alpha Risiko.
Berechnet die Kurtosis einer aus maximal 30 Werten bestehenden Wertereihe.
Berechnet die (kumulierte) Verteilungsfunktion der Lognormalverteilung bis zur Stelle x.
Berechnet den mittleren Wert einer Wertereihe.
Berechnet den Modus einer aus maximal 30 Werten bestehenden Wertereihe
Fortlaufende Ziehung von Elementen aus einer binomialverteilten Grundgesamtheit mit bekanntem Anteil Merkmalsträgern. Man zieht so lange, bis man genau c Merkmalsträger gefunden hat.
NEGBINOMVERT berechnet die Wahrscheinlichkeit, für das Auffinden von genau c Merkmalsträgern genau x "Nicht-Merkmalsräger" zu finden. Beispiele: X
Berechnet
- den Wert der Dichtefunktion der Normalverteilung an der Stelle z (kumuliert = wahr)
- die (kumulierte)
Normalverteilungsfunktion bis zur Stelle z (kumuliert = wahr)
Berechnet die Stelle z auf der horizontalen Achse, die dem kumulierten Flächenanteil der Normalverteilung entspricht. Beispiel: X
Berechnet den Pearson'schen Korrelationskoeffizienten
(= "der" Korrelationskoeffizient)zweier Wertereihen (x-Werte und y-Werte)
Es liege eine poissonverteilte Anzahl Ereignisse/Einheit mit bekanntem Mittelwert vor.
POISSON berechnet die Wahrscheinlichkeit, dass eine Einheit
- genau x Ereignisse enthält (kumuliert = falsch)
- höchstens x Ereignisse enthält
(kumuliert = wahr)
Umkehrfunktion von QUANTILSRANG.
Gibt denjenigen Zahlenwert für eine Wertereihe wieder, sodass der relative Anteil a aller Zahlenwerte der Wertereihe kleiner oder gleich dieses Zahlenwertes ist.
Umkehrfunktion von QUANTIL.
Ermittelt die relative Position a des Wertes x innerhalb einer Wertereihe.
Berechnet den Rang eines Wertes innerhalb einer Gruppe von Werten.
- Richtung = 0 oder leer: Grösster Wert bekommt Rang 1
- Richtung = sonstiger Eintrag: Kleinster Wert bekommt Rang 1
x- und y-Werte sind Wertepare. B ist die Konstante in der Regressionsgeradengleichung y=mx+b. Bei b=0 [j/n] ="falsch" wird b=0 gesetzt.
Stats sind mehrere statistische Kennwerte.
Man beachte, dass x mehrdimensional sein
kann. Dann ist der Befehl RGP als Matrixformel einzugeben.
Für genauere Ausführungen siehe Exceldatei .
In dieser Beispieldatei ist auch der Fall Multiple Regression behandelt (mehrere Wertereihen x, Matrixformel). Beispiel: hier
Wie RGP, jedoch liegt eine Exponentialgleichung zugrunde :
y=b* m1x1*m2x2*…*mnxn, bzw:
ln y = x1 ln m1 + ... + xn ln mn + ln b.
Der einzige, jedoch wichtige Unterschied zu RGP besteht darin, dass die Standardfehler sich auf die Werte ln(mi), ln(b) beziehen.
Berechnet eine lineare Regression aus den bekannten Wertepaaren (x,y) und gibt den daraus geschätzten y-Wert an der Stelle x heraus. Beispiel: X
Berechnet die Schiefe einer aus maximal 30 Werten bestehenden Wertereihe.
Berechnet die Standardabweichung einer Stichprobe.
Erklärung des Unterschiedes STABW - STABWA siehe hier.
Berechnet den standardisierten Wert z einer Normalverteilung mit bekanntem Mittelwert und Standardabweichung. Beispiel: X
Berechnet die kumulierte Standardnormalverteilung zum Wert z. Beispiel: X
Berechnet die Stelle z auf der horizontalen Achse, die dem kumulierten Flächenanteil der Standardnormalverteilung entspricht. Beispiel: X
Berechnet die Steigung der linearen Regressionsgeraden, also den Wert m der Geradengleichung Y =mX + b. Beispiel: X
Schätzt den Standardfehler der auf Basis der x-Werte berechneteten y-Werte bei einer linearen Regression. Beispiel: X
Gibt die Summe der quadrierten Abweichungen von Datenpunkten von deren Stichprobenmittelwert zurück. (Varianz)
Ähnlich wie SCHÄTZER, jedoch berechnet TREND die geschätzten y-Werte für mehrere neuen x-Werte gleichzeitig. TREND ist eine Matrixformel.
J/N = „Wahr“: y-Achsenabschnitt wird aus den gegebenen Daten berechnet.
J/N = „falsch“:
y-Achsenabschnitt wird = 0 gesetzt. Beispiel: X
Berechnet das Alpha Risiko einer t- verteilten Zufallsgrösse. Umkehrfunktion von TINV.
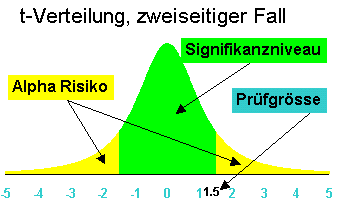
Beispiele: X und hier
Berechnet die Prüfgrösse des zweiseitigen Vertrauensbereichs einer t- verteilten Zufallsgrösse. Umkehrfunktion von TVERT.
Möchte man z.B.den einseitigen 10% Vertrauensbereich, so muss man für das alpha risiko 20% einsetzen. Beispiele: X und hier
TTEST berechnet das Signifikanzniveau dafür, dass die Mittelwerte zweier Stichproben gleich sind.
- Typ 1: gepaarte Werte
- Typ 2: Werte ungepaart, Varianzen gleich
- Typ 3: Werte ungepaart, Varianzen ungleich
Berechnet die Varianz einer aus maximal 30 Werten bestehenden Wertereihe.
Exponentielle Entsprechung zur linearen Funktion TREND.
VARIATION berechnet die geschätzten y-Werte eines exponentiellen Trends für mehrere neue x-Werte gleichzeitig. VARIATION ist eine Matrixformel.
J/N = „Wahr“: y-Achsenabschnitt wird aus den gegebenen Daten berechnet.
J/N = „falsch“: y-Achsenabschnitt wird = 0 gesetzt.
Berechnet die Anzahl Variationen ohne Zurücklegen. Siehe bei Kombinatorik unter "Variation".
Berechnet die gesamte relative Häufigkeit, mit der die Werte der Wertereihe zwischen einer oberen und unteren Grenze liegen. Beispiel: hier
Weibull berechnet die
- Dichtefunktion der Weibullverteilung (kumuliert = falsch)
- Verteilungsfunktion der Weibullverteilung (kumuliert = wahr)
zu einem gegebenen Zeitpunkt. Beispiel: X
Beispiel:
In B10 steht "27"
In E1 steht: "=STABW(B12:INDIREKT(ADDRESSE(12+B10,2)))"
-->
In E1 wird die Standardabweichung aller Werte
berechnet, die in den Zellen B12 bis B39 stehen
(12+27=39)
SVERWEIS
(Suchkriterium, Matrix, Spaltenindex, j/n)
Siehe Beispieldatei für nähere Erläuterungen.
J/N = „Wahr“: Wird keine exakte Entsprechung gefunden, wird die nächstgrössere zurückgegeben.
J/N = „falsch“: Wird keine exakte
Entsprechung gefunden, wird der Fehler N/V zurückgegeben.
Beispiel: ={MITTELWERT(WENN (D3:D35=B42;(WENN(E3:E35=B43;G3:G35))))}
Beispiel