Zeitreihenanalyse bewertet vergangene Daten und extrapoliert in die Zukunft. Das häufigste Modell dafür ist das ARIMA Modell, AutoRegressive Integrated Moving Average Modell.
ARIMA
AutoRegressive Integrated Moving Average Modell.
Dieses Modell dient zur Beschreibung von Datenreihen in der Zeitreihenanalyse und ist so allgemein, dass es mehrere unter anderem Namen bekannte Methoden als Spezialfälle enthält. Das hier vorgestellte Modell ist additiv, das heisst, die einzelnen Komponenten addieren sich zum Gesamtergebnis.
Im Gegensatz dazu steht das Multiplikative Modell.
Aufgrund der Komplexität dieses Modells und der zahlreichen Varianten und Erweiterungsmöglichkeiten kann hier nur das Grundgerüst auf anschaulicher Ebene wiedergegeben werden. Für konkrete Berechnungen rät der Verfasser unbedingt zu einschlägiger Literatur und Software.
Die hier dargestellten Rechenwege sind derart, dass sie im Kopf nachvollzogen werden können; sie führen aber mit grosser Wahrscheinlichkeit nicht zu den optimal erzielbaren ARIMA Modellen.
Ziel der aus den 3 Parametern p,d,q bestehenden Methode ARIMA(p,d,q) ist es:
Die vorliegende Messreihe vollständig zu beschreiben
Dies ist nach dem Theorem von Wold für alle stationären Zeitreihen möglich.
zukünftige Werte der Zeitreihe vorherzusagen.
Dies funktioniert deshalb, weil der jeweils aktuelle Wert mittels Kombination von Einflüssen vorangehender Werte beschrieben wird.
Es handelt sich hier um eine mathematische Zerlegungsmethode. Vom Grundgerüst her ist das vergleichbar beispielsweise mit
Taylorreihen (Darstellung einer beliebigen Funktion mit einem Polynom)
Fourierreihen (Darstellung einer beliebigen Funktion
mit Sinus oder Cosinusfunktionen)
ARIMA arbeitet mit 2 Komponenten
einer gewichteten Summe aus zurückliegenden Messwerten (AR, AutoRegressive, Schritt2)
einer gewichteten Summe aus zurückliegenden Zufallseinfluessen (MA, Moving Average, Schritt 3).
Diese beiden Komponenten ergeben strenggenommen "nur" ein ARMA Modell (ohne "I", Schritt 1).
Der Buchstabe I (Integrated) symbolisiert die Sicherstellung der
Nahezu alle statistischen Verfahren verlangen stationäre, also sich nicht ändernde Randedingungen.
Im Falle von Zeitreihen bedeutet Stationarität, dass die zugrundegelegte Verteilungsfunktion der Messwerte zeitlich konstant ist.
Die Nicht-Erfüllung dieser Voraussetzung sei anhand folgender Beispiele veranschaulicht:
| Hier nimmt offensichtlich der Mittelwert mit der Zeit zu | Zeitreihen mit (nicht nur linearem) Trend können mit dem ARIMA Modell unter Umständen erfolgreich beschrieben werden. | |
| Hier nimmt offensichtlich die Varianz mit der Zeit zu | Zeitreihen mit veränderlicher Varianz und veränderlicher höherer Momente können mit der ARIMA Methode nicht beschrieben werden. |
Eine stationäre Zeitreihe besteht also aus Werten, die entsprechend der zugrundegelegten Verteilungsfunktion um einen zeitlich konstanten Mittelwert streuen.
Interessant ist hier, dass die einzelnen Werte- obwohl aus einer konstant bleibenden Verteilungsfunktion stammend- nicht voneinander unabhängig zu sein brauchen. In solchen Fällen macht die Vorhersage zukünftiger Werte sogar erst richtig Sinn.
Beispiel:
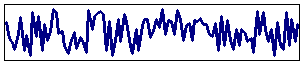 |
Dies könnte ein Zufallsrauschen sein, dem ein langwelliges Schwingungsgemisch überlagert ist. |
Die Funktionsweise des ARIMA Modells soll im Folgenden schrittweise erarbeitet werden.
Anmerkung: Es wird davon ausgegangen, dass saisonale Effekte bereits herausgerechnet worden sind.
Die Berücksichtigung saisonaler Effekte gehört eigentlich nicht zum ARIMA Modell.
Schritt 1: Herstellung von Stationarität: Trendbeseitigung
Besitzt die zu untersuchende Zeitreihe einen Trend, dann muss dieser also zuerst beseitigt werden.
Da man zur Vorhersage von Messwerten immer die Originalreihe vor Augen haben muss, ist es ratsam, zur Erreichung von Stationarität möglichst "einfache" mathematische Operationen zu verwenden, die man leicht wieder rückgängig machen kann.
Hat der Trend die Form eines Polynoms n-ter Ordnung:
dann lässt er sich einfach durch n-faches Differenzieren beseitigen
Aus Sicht des ARIMA Modells ist die Originalmessreihe folglich integriert (Integrated).
Beispiel 1:
Nach 2facher Differenzierung (Abziehen jeweils benachbarter Werte) einer Reihe mit offenbar quadratischem Trend erhält man eine Reihe, die offenbar keinen Trend mehr enthält. (Rauschen wurde der Übersicht halber weggelassen)
Saisonale Schwankungen (Periodizität) sind eine weitere Verletzung von Stationarität.
Sie lassen sich dadurch beseitigen, indem man im ersten Differezierungsschritt nicht jeweils benachbarte Werte voneinander abzieht, sondern zB. den 6. vom 1., den 7. vom 2., den 8. vom 3., usw. (In diesem Beispiel besteht die Periodendauer aus 5 Messwerten)
Anschliessend kann -falls notwendig- wieder "normal", also zwischen jeweils benachbarten Werten differenziert werden.
Saisonale Schwankungen lassen sich aber auch durch die autoregressive Komponente (AR) beschreiben, welche im nächsten Schritt beschrieben wird.
Waren im konkreten Fall beispielsweise 2 Differenzierungen zur Erreichung von Stationarität notwendig, dann muss man zur Vorhersage bezüglich der Originalreihe erst wieder 2 mal integrieren.
Formal wird dieser Fall als ARIMA(p,d,q) mit d=2, also ARIMA(p,2,q) bezeichnet.
Schritt 2: AutoRegressive Komponente: Vorhersage mittels zurückliegender Messwerte.
Ergebnis dieses Schrittes ist eine Gleichung der Form
![]() ,
,
der n-te Wert hängt also von einer Reihe vorausgegangener Werte ab. (Rauschen wurde hier weggelassen)
Um die Koeffizienten an-i zu ermitteln wird zunächst der Korrelationskoeffizient zwischen der stationär gemachten Messreihe und der um i Messwerte verschobenen stationär gemachten Messreihe (sogenanntes "i-tes Lag") berechnet.
Beispiel 2 (hat nichts mit Beispiel 1
zu tun)
Folgende Grafik visualisiert die Tabellenwerte:
In der rechten Spalte der Tabelle (rot) stehen die Korrelationskoeffizienten zwischen der stationär gemachten Originalreihe und ihrem 1. bis 5. Lag.
Es ist nicht auszuschliessen, dass es unter den noch höheren Lags einige mit ebenfalls bedeutsamen Korrelationskoeffizienten gibt.
Bei der Berechnung der Korrelationskoeffizienten wird nicht zyklisch gerechnet (wie bei der Autokorrelation), sondern es werden nur übereinanderstehende Werte verwendet. Das bedeutet, dass die Anzahl Wertepaare für höhere Lags geringer wird.
Folgende Tabelle zeigt die Berechnungen der Signifikanz der Korrelationskoeffizienten.
Das genaue Vorgehen hierzu ist unter der Rubrik Z-transformation beschrieben.
Die Tabelle zeigt 5 einzeln und unabhängig durchgeführte Tests. Zur hier auftretenden Problematik siehe Multiples Testen und Alpha Inflation. Wir könnten hier an dieser Stelle entscheiden, dass der 1. und 4. Lag zur Modellierung ausreichen.
Genausogut könnten wir auch alle 5 Komponenten im weiteren Modell hinzunehmen.
Beide Fälle sind in folgender Grafik dargestellt.
Man sieht, dass die Hinzunahme der Lags 2,3 und 5 nicht unbedingt das bessere Modell ergibt.
| Die Berechnung erfolgte so, dass die Summe der quadrierten Korreletionskoeffizienten der jeweils verwendeten Lags zu Eins normiert und gewichtet worden ist. | |
|
Die bisher ermittelten Modellgleichungen der beiden Modelle lauten: ARIMA(4,2,q): ARIMA(5,2,q):
Hier ist 5.2 der Mittelwert der Originalreihe. Die Werte der anderen Vorfaktoren ergeben sich aus den normierten Bestimmtkeitsmassen (=quadrierte Korrelationskoeffizienten) der Lags, wobei die Vorzeichen von den Korrelationskoeffizienten übernommen wurden. Folgend Tabelle veranschaulicht den Rechengang: |
|
Es ist zu bedenken, dass die Signifikanzwerte in der Tabelle keine Verbindung mit einem mehr oder weniger guten Modell haben. Sie bedeuten lediglich, dass die Korrelationskoeffizienten "nicht bloss Zufall" sind.
Ausserdem
wurde hier nicht berechnet, wie Lag 4 direkt mit der stationär gemachten Originalreihe korreliert, da der hier berechnete Korrelationskoeffizient alle Einflüsse der Lags 1, 2, 3 und 4 beinhaltet.
Diese Art Korrelation heisst partielle Autokorrelation und wird hier nicht behandelt.
Es gibt spezielle Signifikanztests, die auf Autokorrelation testen.
Durbin h-Statistik: Testet die Autokorrelation der Zeitreihenwerte mit dem ersten Lag.
Durbin Watson Test: Testet die Autokorrelation der Residuen der Zeitreihenwerte mit dem ersten Lag.
Testet also auf Autokorrelation der Fehler --> Schritt 3.
Ljung-Box Test: Testet alle Lags auf einmal.
Schritt 3: Moving Average: Vorhersage mittels vorangegangener Fehler.
Unter "Fehler" ist hier zufälliger statistischer Einfluss zu verstehen, denn eine stationäre Zeitreihe besteht aus Werten, die entsprechend der zugrundegelegten Verteilungsfunktion um einen zeitlich konstanten Mittelwert streuen.
Ergebnis dieses Schrittes ist eine Gleichung der Form
.
Die autoregressive Komponente des vorhergehenden Schrittes 2 wird also mit gewichteten Fehlern vorangehender Werte korrigiert.
Folgende Tabelle enthält in der obersten Zeile die stationär gemachte Originalreihe aus Beispiel 2, in der 2. Zeile das AR Modell aus Schritt 2, dann den Fehler des Modells aus Schritt 2, und schliesslich die ersten 5 Lags des Fehlers (also die Wertereihe des Modellfehlers um 1,2,3,4 und 5 Positionen verschoben).
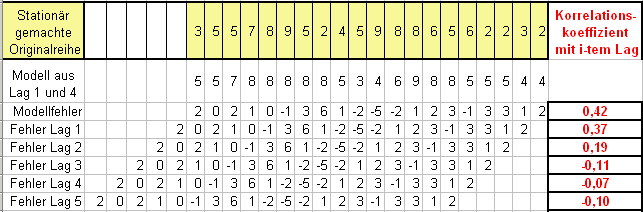
Ohne explizite Rechnung ist bereits erkennbar, dass keiner der Korrelationskoeffizienten signifikant ist, ja sogar jeder relativ klein ist. Das deutet stark darauf hin, dass der Fehler des in Schritt 2 gewonnenen Modells fast nur aus zufälligem (normalverteiltem) Rauschen besteht.
Das bedeutet konkret:
Der n+1 -te Messwert wird durch keine Zufallskomponente irgendeines vorhergehenden Wertes n, n-1, ...n-s beeinflusst
Die Fehler korrelieren nicht einmal mit den Werten selbst (0.20)
Es gibt in der vorliegenden Reihe keine Fehlerfortpflanzung.
Das bisher entwickelte Modell lautet demnach ARIMA(4,2,0)
4: Der autoregressive Teil des Modells (AR) greift bis auf den 4. Lag zurück
2: Die Originalreihe musste 2 Mal differenziert werden, um stationär zu werden.
0: Der Moving Average Teil (MA) greift auf keinen Lag zurück.
Im
Folgenden seien zum allgemeinen Verständnis bildhaft ein paar "schöne"
Autokorrelationsfunktionen und partielle Autokorrelationsfunktionen
sowie die dazugehörende Nomenklatur dargestellt.
Die
Säulen stellen Korrelationswerte dar.
Bei
Autokorrelationsfunktionen, ACF,
handelt es sich um Funktionen wie bisher
beschrieben, d.h., es werden alle Einflüsse berrücksichtigt. In dem
obigen Beispiel 2 wurde zwar entschieden, nur Lag 1 und 4 für das zu
erstellende Modell zu verwenden, trotzdem sind dort die eventuellen
Einflüsse der Lags 2 und 3 mit enthalten, denn Lag 4 kann ja von Lag 3
abhängen, und Lag 3 von Lag 2, und dieses wiederum von Lag 1;
alternativ könnte Lag 4 aber auch direkt
von Lag 1 abhängen und nicht von Lag 2 und 3, wieder alternativ könnte
Lag 4 von allen Lags 1,2 und 3 abhängen; die bisher beschriebene
Vorgehensweise zur Bildung
der Autokorrelationsfunktion kann diese Fälle grundsätzlich nicht
unterscheiden (ob Lags direkt voneinander abhängen oder über
dazwischenliegende Lags).
Aus
diesem Grund verwendet man Partielle Autokorrelationsfunktionen,
PACF: Dort berechnet man
z.B.den direkten Einfluss des Lags 4 auf die
originale Messreihe und rechnet die Einflüsse der Lags 1,2 und 3 auf
Lag 4 heraus.
Die blosse visuelle Analyse der beiden Funktionen ACF(pdq) und PACF(pdq) erlaubt in vielen Fällen bereits richtungsweisende Aussagen.
Allerdings erfordert bereits die Erstellung der beiden Funktionen schon spezielle Statistiksoftware.
| Autokorrelationsfunktion (ACF) | Partielle Autokorrelationsfunktion (PACF) | |
| Beschreiben den "Zusammenhang" der originalen Messreihe mit allen ihren Lags | ||
|
Die Einflüsse dazwischenliegender Lags sind in den Autokorrelationswerten...... |
||
| .....enthalten |
.....NICHT enthalten. Sie werden herausgerechnet. |
|
 |
Weisses (normalverteiltes)
Rauschen.
Die Werte sowie ihre Fehler beeinflussen sich nicht. Kein Lag korreliert mit einem anderen Lag. |
 |
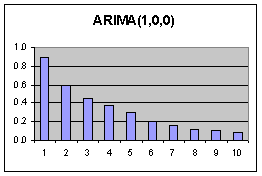 |
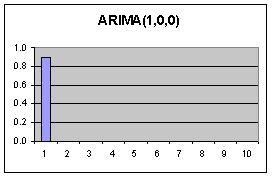
Jeder Wert
wird ausschliesslich durch seinen unmittelbaren Vorgänger beeinflusst.
(Nur 1 Mode im PACF Diagramm)
Dadurch entstehen Korrelationen über mehrere Lags hinweg (Abfallende Moden im ACF Diagramm, ab der ersten Mode) Die Fehler beeinflussen sich nicht. |
 |
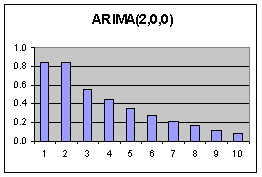 |
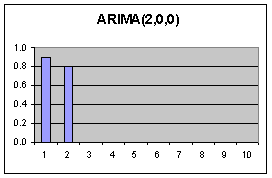
Jeder Wert
wird ausschliesslich durch seine 2 unmittelbaren Vorgänger beeinflusst.
(Nur 2 Mode im PACF Diagramm)
Dadurch entstehen Korrelationen über mehrere Lags hinweg (Abfallende Moden im ACF Diagramm, ab der 2. Mode) Die Fehler beeinflussen sich nicht. |
 |
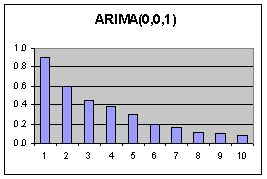
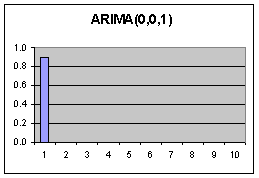 |
Jeder Wert
wird nur durch den Fehler
seines unmittelbaren Vorgängers beeinflusst.
(Nur ein Mode im ACF Diagramm).
Dadurch entstehen Korrelationen der Werte über mehrere Lags hinweg (Abfallende Moden im PACF Diagramm) Die Werte an sich beeinflussen sich nicht. Die Korrelationen entstehen durch Fortpflanzung der Fehler. |
 |
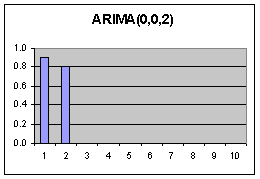 |
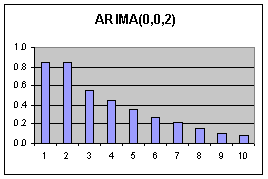
Jeder Wert wird nur durch die Fehler seiner 2 unmittelbaren Vorgänger beeinflusst. (Nur 2 Moden im ACF Diagramm). Dadurch entstehen Korrelationen der Werte über mehrere Lags hinweg (Abfallende Moden im PACF Diagramm) Die Werte an sich beeinflussen sich nicht. Die Korrelationen entstehen durch Fortpflanzung der Fehler.
|
 |
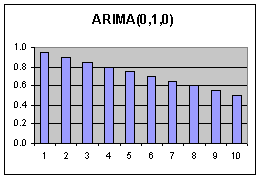 |
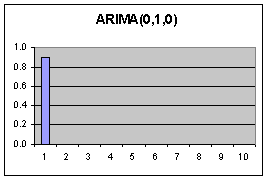
Die Moden im ACF Diagramm fallen LINEAR ab. Es handelt sich offenbar um eine linear ansteigende Zeitreihe. (Stationarität nicht gegeben) Folglich wird jeder Wert zwangsläufig durch Vorgänger beeinflusst. Hier ist es nur der unmittelbare Vorgänger (Nur 1 Mode im PACF Diagramm) Bei einmaligem Differenzieren dieser Reihe würden beide Diagramme keine Moden mehr zeigen. |
 |
20.12.2018