Mathematisch gesehen = Odds Ratio.
In der medizinischen Diagnostik speziellere Bedeutung:
"Um wie viel mal häufiger kommt ein positives (negatives) Testresultat bei Personen mit Erkrankung im Vergleich zu Personen ohne Erkrankung vor".
Allgemein einsetzbares Verfahren zum Vergleich von Modellen auf der Grundlage der Maximum Likelihood Estimation.
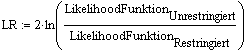
Unrestringiert meint das vorliegende Modell mit noch allen Parametern.
Restringiert bedeutet, dass ein(ige) Parameter auf einen bestimmten Wert (z.B. =0) festgesetzt wurden, also als Parameter aus dem Modell ausscheiden.
Ziel ist es, ein möglichst einfaches Modell ohne wesentlichen Verlust an Erklärungskraft zu finden, oder umgekehrt mit möglichst wenig hinzugenommenen Parametern einen signifikanten Gewinn an Erklärungskraft zu erhalten.
Erklärungskraft meint hier den Quotienten (Aufgeklärte Varianz/Gesamtvarianz)
Das Likelihood Ratio LR ist Chi Quadrat verteilt mit k Freiheitsgraden, wobei k die Anzahl der Restriktionen ist.
Aufgrund von 3. häufig angewandte Methode zur Berechnung von Vertrauensintervallen.
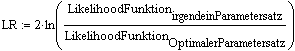
Der optimale Parametersatz repräsentiert die Punktschätzung desjenigen
Parametersatzes, für den die Ziehungs w
Das Likelihood Ratio LR ist Chi Quadrat verteilt mit k Freiheitsgraden, wobei k die Anzahl der Parameter ist.
Bei der Ermittlung von Vertrauensbereichen wird im gesamten Parameterraum derjenige Teilraum gesucht, für den das Likelihood Ratio LR grösser ist als die kumulierte Chi Quadrat Verteilung zum Niveau a,
das heisst, mit den Parametern der Likelihood Funktionirgendein Parametersatz wird so "herumgespielt", dass man möglichst "alle" Parameterkonstellationen erhält, die grösser sind als die Chi Quadrat Verteilung zum Niveau a.
Bei Funktionen mit 2 Parametern sind dies zweidimensionale Gebiete.