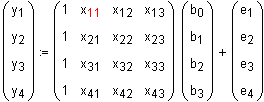 oder
in Matrixschreibweise:
oder
in Matrixschreibweise:
Multiple lineare Regression mit Excel Beispiel
Der Unterschied multiple Korrelation <-> multiple Regression ist der selbe wie der Unterschied Korrelation <-> Regression.
Es folgt zunächst eine allgemeine Betrachtung.
Zum konkreten Rechenbeispiel einschliesslich Konfidenzintervallen geht es hier.
Für eine (multiple) lineare Regression in Excel siehe hier.
Die (multiple) lineare Regression mehrerer Variablen auf eine andere Variable ist eine Schätzung einer abhängigen Variablen mit Hilfe mehrerer unabhängiger Variablen unter der Annahme linearer Zusammenhänge.
Die Voraussetzungen sind die selben wie im allgemeinen linearen Modell,
die Matrix wird jedoch um eine Spalte Einsen erweitert, um dem konstanten Faktor b0 bei der linearen Regression Rechnung zu tragen (Ein (!) konstanter Faktor für das gesamte Modell).
Möglichst geringe Kollinearität ist ebenfalls wichtige Voraussetzung bei der Durchführung einer Regressionsanalyse.
In den Folgenden Schritten sei aus Gründen der Anschaulichkeit ein Modell angenommen mit 3 unabhängigen Variablen xj (j=1..3) , ferner seien 4 Messungen vorgenommen worden (i=1....4). Es gibt folglich 4 mal einen Messfehler ei (i=1...4).
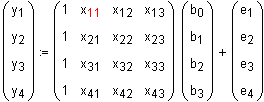 oder
in Matrixschreibweise:
oder
in Matrixschreibweise: ![]()
yi : i-te Realisierung der (einen (!)) abhängigen Variablen y,
xij: i-te Realisierung der j-ten unabhängigen Variablen xj,
bj j-ter unbekannter (zu bestimmender) Modell parameter (Steigung der Geraden j),
ei i-ter unbekannter Fehler e.
Für die erste Messung der Variable y sieht das ausgeschrieben wie folgt aus:
![]()
Entsprechendes gilt für die restlichen Messungen.
Ziel der multiplen linearen Regression ist die Bestimmung der Modellparameter b0, b1, b2,....bn.
Diese sind mit einem Fehler behaftet, denn würde man die gesamten Messungen wiederholen, so bekäme man dann sicherlich etwas andere Werte für b0, b1, b2,....bn.
Nun
kann man allein aufgrund der Messdaten Intervalle für die
Parameter b0, b1, b2,....bn angeben, innerhalb derer die
"wahren" Werte b0, b1, b2,....bn
mit einer bestimmten
Dazu berechnet man deren Varianz und erhält dann mit Hilfe der Normalverteilung die jeweiligen Vertrauensintervalle.
Da die Modellparameter nicht unabhängig voneinander variieren, müssen zusätzlich noch alle Kovarianzen der Modellparameter untereinander berechnet werden (also b0 mit b1, b0 mit b2,......,b1 mit b2,.......).
Dies wird formal durch die Varianz-Kovarianzmatrix dargestellt:
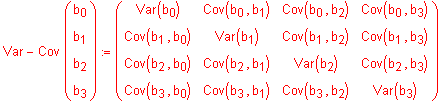
Die Varianz-Kovarianzmatrix ist symmetrisch bezüglich ihrer Diagonalen, da die Kovarianz zwischen 2 Variablen (a,b) oder (b,a) unabhängig von deren Reihenfolge ist.
Die Varianz-Kovarianzmatrix berechnet sich aus den Messwerten formal und allgemein mit Hilfe des Produktes
[(Transponierte Matrix Xij) * (Matrix Xij)]-1 * (Fehlervarianz), also:
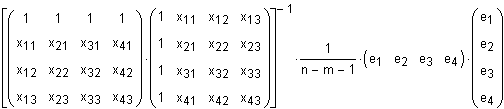
n: Anzahl Realisierungen, Messungen (hier: 4)
m: Anzahl unabhängiger Variablen (hier: 4; b0.....b3)
Der Bruch 1/(n-m-1) ist die Anzahl Freiheitsgrade.
Zu einem konkreten Rechenbeispiel einschliesslich Konfidenzintervallen geht es hier.
Möglichst geringe Kollinearität ist wichtige Voraussetzung bei der Durchführung einer Regressionsanalyse.
Wichtige Voraussetzung bei der Berechnung der Vertrauensintervalle ist Varianzhomogenität.
Diese kann man mit dem White Test überprüfen.
Für eine (multiple) lineare Regression in Excel siehe hier.
Ein Test, der das Regressionsmodell hinterfragt, ist der Chow Test.