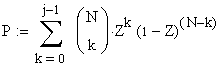Das Weibullnetz ist eine graphische Methode zur Bestimmung der beiden Parameter (charakteristische Lebensdauer und Formparameter) bei weibullverteiltem Datenmaterial.

Die während der Tests angefallenen Lebensdauerdaten müssen vor der Eintragung in ein Weibullnetz jedoch aufbereitet werden.  

Früher arbeitete man hauptsächlich mit speziell erhältlichem Weibullpapier, welches im Wesentlichen ein Koordinatennetz mit "spezieller" Skalierung der beiden Koordinatenachsen ist. Die Art der Skalierung ist so, dass bei tatsächlichem Vorliegen einer Weibullverteilung die in das Netz eingetragenen Datenpunkte genau auf einer Geraden liegen.

Aufgrund der Lage der Geraden und mit einer dritten Skala, meistens rechts als zweite y-Achse angebracht, konnten sowohl die charakteristische Lebensdauer als auch der Formparameter leicht abgelesen werden:

• Die Charakteristische Lebensdauer ergibt sich als Schnittpunkt der an die Datenpunkte angepassten Geraden mit der horizontalen Geraden, die durch den 63,2% Punkt der vertikalen Achse geht. (63,2% =1- 1/e)

• Den Formparameter erhält man, indem man eine zur angepassten Geraden parallele Gerade zeichnet, welche durch einen speziell markierten Punkt ("Pol") gehen muss, und eine eigens hierfür eingerichtete zweite vertikale Achse schneidet. Der darauf abgelesene Schnittpunkt ist der Formparameter.

Obwohl dies alles heutzutage mit Hilfe geeigneter Software durchgeführt wird, sind der Rechenweg und die visuelle Darstellung im Weibullnetz in weiten Bereichen gleich geblieben. 

Wesentlicher Vorteil bei der Verwendung von Software liegt abgesehen von der einfacheren Bedienung in der Berechnung von Vertrauensintervallen.

Zurück zum Glossar (Weibullnetz)

Weibullnetz

Unterabschnitte: 

0. Vorbereiten des Datenmaterials

1. Beispiel 1: Nicht-zensorisierte Daten

2. Beispiel 2: Zensorisierte Daten

3. Beispiel 3: Sudden Death Verfahren

4. Generelle Anmerkungen zur Anpassungsgüte

0. Vorbereiten des Datenmaterials

Die während der Tests angefallenen Lebensdauerdaten müssen vor der Eintragung in ein Weibullnetz  mit Hilfe der folgenden Schritte aufbereitet werden.  

1. Sortieren der Ausfallzeitpunkte nach aufsteigender Reihenfolge (also früheste Ausfälle zuerst)  

2. Ermitteln der Rangpositionen (0.....1) nach einer der folgenden gebräuchlichen Methoden: 

   (Eilige Leser mögen sich mit der gelb unterlegten Variante begnügen. Diese Variante wird bei den meissten Weibullanalysen angewendet). Die grün hinterlegte Variante ist die exakte. 

    

   Bezeichnung	Formel	Erklärung
   California Relationship	k/N    [bei klassierten Daten ist diese Formel zu wählen]	N: Grösse der Testpopulation.  k:   Nummer des Ausfalls   Dem k-ten Ausfallpunkt wird die kumulierte Ausfallhäufigkeit entsprechend der verwendeten Formel zugewiesen.
   Benard’s median ranks	(k-0.3)/(N+0.4)  Dies ist eine Näherung für P=0.5 (siehe weiter unten: Beta Binomiale vertrauensintervalle)
   Hazen plotting position	(k-0.5)/N
   Weibull’s mean rank	[k/(N+1)]
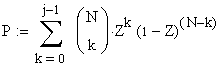
   Exakte Beta-Binomiale median ranks.  Dies ist die exakte Methode. Einzelheiten dazu siehe unter Beta Binomiale Vertrauensintervalle	Achtung: Z ist die gesuchte Variable.  N,k und P sind gegeben.	P: Vertrauensintervall (einseitig) für die relative kumulierte Häufigkeit beim k-ten Ausfall  Z: Rangposition beim k-ten Ausfall (gesuchte kumulierte Ausfallhäufigkeit).  j: Ordnungsnummer Benard's Median Ranks sind eine Näherung der Z für P=0,5. N: Grösse der Testpopulation.   k: Nummer des Ausfalls
   Mit dem Solver in Excel kann man die z-Werte für gegebene P bestimmen lassen. Siehe hierzu diese Exceldatei. Ausführlichere Erklärungen hierzu befinden sich unter Beta Binomiale Vertrauensintervalle.

3. Eintragen der Wertepaare (Ausfallnummer | Rangposition) in das Weibullnetz. 

   In der Literatur gibt es Tabellen für die Rangpositionen im Abhängigkeit der Anzahl Individuen, sodass nicht mir zuvor stehenden Formeln gerechnet werden muss. ferner gibt es hinreichend Softwareprogramme, die dem Benutzer die Rangproblematik komplett abnehmen.

4. Ablesen der beiden Parameter "Lebensdauer" und "Formfaktor" (siehe Weibullverteilung)

   • Lebensdauer: Schnittpunkt der Näherungsgeraden mit der zur kumulativen Ausfallhäufigkeit 63,2% gehörenden horizontalen Linie. 

   • Formfaktor (Ausfallsteilheit): Schnittpunkt der zur Näherungsgeraden parallelen, jedoch durch den Punkt "Pol" gehenden Geraden mit der rechten vertikalen Skala. 

     Anmerkung: Kommerzielle Softwarepakete berechnen beides automatisch.

Beispiel 1: Nicht zensorisierte Daten 

N=12; 10 davon bisher ausgefallen.

Weibull Lebensdauernetz für das Beispiel Nicht zensorisierte Daten mit unterer 90% Vertrauensgrenze.

Die untere Vertrauensgrenze ist diejenige Kurve, bezüglich der die "wahre" (aber unbekannte) Gerade mit 90% Wahrscheinlichkeit rechts davon liegt.

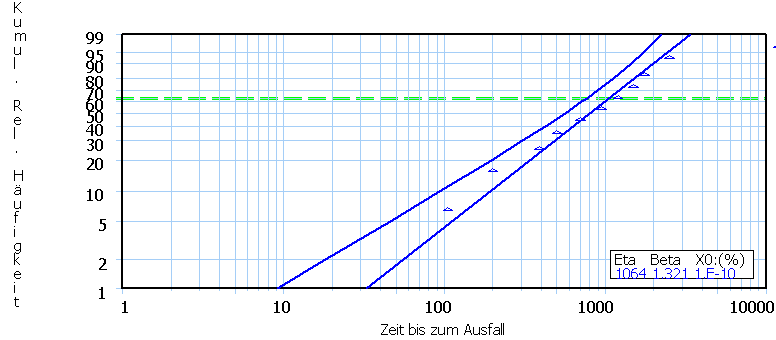
Für Eta als charakteristische Lebensdauer ergibt sich 1064. Die Ausfallsteilheit beträgt 1,321.

Bei zensorisierten Daten kommt das Johnson Verfahren zur Anwendung.  Dieses berücksichtigt 2 Sachverhalte: 

• Die zensorisierten Daten erhöhen die kumulierte Lebensdauer,

• Die zensorisierten Daten verringern den jeweiligen Bestand.

Beispiel 2: Zensorisierte Daten   

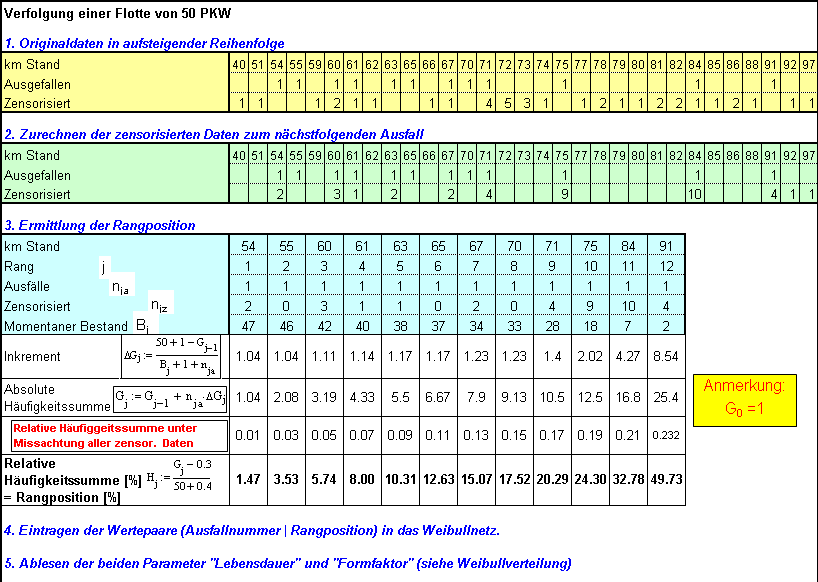
Weibull Lebensdauernetz für das Beispiel zensorisierte Daten mit unterer 90% Vertrauensgrenze.

Die Vertrauensgrenze ist die Einhüllende, innerhalb der die "wahre" (aber unbekannte) Gerade mit 90% Wahrscheinlichkeit liegt.

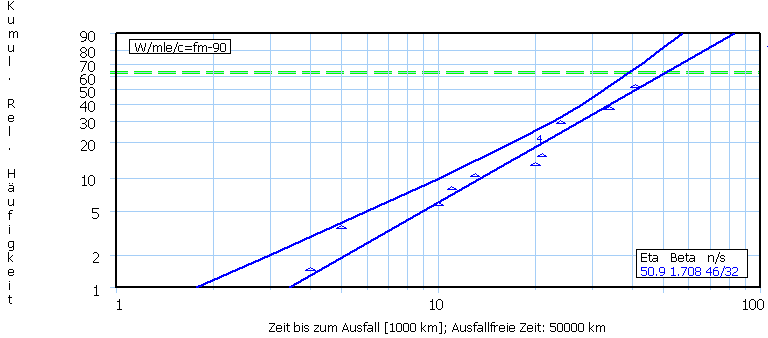
Man beachte, dass hier 50.000 km ausfallfreie Zeit mit berücksichtigt sind, d.h.: für Eta als charakteristische Lebensdauer egribt sich 50.9 + 50 = 109000 km. Die Ausfallsteilheit beträgt 1,708.

Hätte man in obigem Beispiel die zensorisierten Daten einfach ignoriert, dann würde man ein falsches Ergebnis bekommen: 

• Ginge man von einer Population von 12 aus, dann wäre die letzte Rangposition anstatt 49.73% bei über 94%, und somit die ermittelte Lebensdauer zu gering. 

• Ginge man von einer Population von 50 aus, dann wäre die letzte Rangposition anstatt 49.73% bei nur 23%, und somit die ermittelte Lebensdauer zu hoch. 

Beispiel 3: Sudden Death 

Eine Population wird in kleine Gruppen unterteilt. Die jeweils ersten Ausfälle pro Gruppe werden notiert. 

Die Unterteilung in Untergruppen macht man nicht aus Prinzip, sondern ist durch die Art des Testmaterials vorgegeben, wie folgendes Beispiel zeigt. 

Beispielskizze:

Lebenserwartung von Einlassventilen bei Vierzylindermotoren. Bei Ausfall des ersten von 4 Ventilen ist der gesamte Motor defekt; 

die Ausfälle der weiteren 3 Ventile können aus technischen Gründen nicht mehr "ertestet" werden. 

Man trägt hier die jeweils ersten Ausfälle anhand der exakten beta binomialen median ranks auf , wobei hier P= 0.25 zu setzen ist (ein Viertel, weil 4 Ventile/Einheit). 

Schliesslich verschiebt man die gesamte gewonnene Kurve im Weibullnetz soweit nach rechts, wie es den Median Ranks entsprechen würde (P=0,5) 

Ausführlichere Erklärungen zu den P-Werten befinden sich unter Beta Binomiale Vertrauensintervalle.

Generelle Anmerkungen zur Anpassungsgüte.

Die Güte der Anpassung kann angegeben werden mittels

• Korrelationskoeffizient

  Dies ist möglich, weil die Achsen ja so skaliert werden, dass die zugrundegelegte Verteilungsfunktion (hier Weibullverteilung) eine Gerade ergibt.

  Liegt der Korrelationskoeffitient "nahe bei" +1, dann gilt die Anpassung durch die zugrundegelegte Verteilungsfunktion als gut.

  Dies bedeutet aber nicht zwangsläufig, dass das Datenmaterial auch wirklich vom zugrundegelegten Verteilungsfunktionstyp ist, selbst wenn der Korrelationskoeffizient  bei +0,99 liegen sollte.

  Diesem Sachverhalt wird durch den sogenannten Kritischen Korrelationskoeffizienten Rechnung getragen.

  Für nähere Erläuterungen siehe kritischer Korrelationskoeffizient, 2.

   

  Der kritische Korrelationskoeffizient wird von  manchen Weibull Softwarepaketen mitberechnet.

   

• Likelihood Ratio

  Dabei werden die Likelihood Funktionen zweier prinzipiell in Betracht kommenden Verteilungsfunktionstypen miteinander verglichen.

  Die übergeordnete Methode heisst Maximum Likelihood Estimation.

  Im Gegensatz zum kritischen Korrelationskoeffizienten kann mit dieser Methode nur eine relative Anpassungsverbesserung im Vergleich zu einer anderen Verteilungsfunktion angegeben werden, aber keine absolute Anpassungsgüte.

• Anpassungstest mittels Anderson Darling Test.

  Dieser Test überprüft explizit die Nullhypothese "Die Daten sind weibullverteilt". 

Tests, die speziell auf sich ändernde Ausfallraten testen, befinden sich hier. 

01.09.2005

Zurück zum Glossar (Weibullnetz)