Beta Binomiale Vertrauensintervalle
Verteilungsfunktionsfreie, rangbasierte Methode zur Abschätzung von Vertrauensintervallen.
(Siehe auch Schätzen)
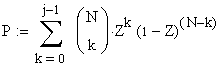
Dies ist nichts Anderes als die (kumulierte) Binomialverteilung.
N: gesamte Anzahl Messwerte,
P: Vertrauensgrenze (typischerweise 90% oder grösser)
k: Nummer des Messwertes
j: Ordnungsnummer
Z: Rangposition, dies ist die gesuchte Variable.
Die wichtigste praktische Anwendung der obigen Formel ist die Ermittlung der Rangpositionen, die man zum Eintragen der Ausfälle in ein Weibullnetz braucht. Es sei vorab betont, dass obige Formel nicht mit der Weibullverteilung in Verbindung steht, sondern dass sie universell für alle Verteilungsfunktionsarten gilt. Die folgende Erklärung bezieht sich dennoch auf die Weibullverteilung.
1.)
Nehmen wir an, wir hätten einen Test laufen, mit dem wir die Lebensdauer von Bauteilen bestimmen wollten.
Der Test sei schon eine Weile gelaufen und es sind inzwischen bereits 2 der insgesamt 10 Bauteile ausgefallen.
Unabhängig davon, ob die Ausfallrate sich zeitlich ändert, ist der momentane Zustand (2 Ausfälle) ein Zufallsereignis, bei dem jedes der 10 Bauteile die selbe Wahrscheinlichkeit hatte, auszufallen.
Diese Einzelwahrscheinlichkeit p kann man nicht eindeutig berechnen, da man ja die nicht weiss, wie optimistisch oder pessimistisch die 2 von 10 Ausfälle die (unbekannte!) Realität wiedergeben.
Die Einzelwahrscheinlichkeit p ist gleich dem Anteil der Gesamtpopulation, der zum Zeitpunkt "2 von 10 ausgefallen" bereits ausgefallen ist. Intuitiv liegt nahe, dass p hier = 0,2 sein muss.
Betrachten
wir aber einmal die folgenden
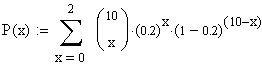 = 0,67
= 0,67 |
Bei einer Eintrittswahrscheinlichkeit
eines einzelnen Ereignisses von p=0,2 ist die Wahrscheinlichkeit, dass
bei 10 möglichen Ereignissen bis zu 2
(also 0,1 oder 2)
auftreten, gleich P=0,67. Das ist gleichbedeutend mit Folgendem: In
einer Urne seien 20% rote Kugeln und der Rest schwarze Kugeln. Man
zieht 10 Kugeln. Die Wahrscheinlichkeit, bis zu 2 (also 0, 1 oder 2) rote gezogen zu haben, liegt bei 67%. --> Die intuitiv zu 0,2 geschätzte Einzelwahrscheinlichkeit ist zu optimistisch. In mehr als 50 % aller Fälle (67%) würde man 2 von 10 Ausfälle vorliegen haben. |
| |
Bei einer Eintrittswahrscheinlichkeit eines einzelnen Ereignisses von p=0,258 ist die Wahrscheinlichkeit, dass bei 10 möglichen Ereignissen bis zu 2 (also 0,1 oder 2) auftreten, gleich P=0,5. Das ist gleichbedeutend mit Folgendem: In einer Urne seien 25,8% rote Kugeln und der Rest schwarze Kugeln. Man zieht 10 Kugeln. Die Wahrscheinlichkeit, bis zu 2 (also 0, 1 oder 2) rote gezogen zu haben, liegt bei 50%. --> Wenn die 2 von 10 Ausfälle "in etwa" der unbekannten Realität entsprechen (P=0.5) , dann liegt die Einzelwahrscheinlichkeit bei p=0,258.
|
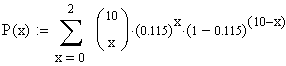 =
0,9 =
0,9 |
Bei einer Eintrittswahrscheinlichkeit eines einzelnen Ereignisses von p=0,115 ist die Wahrscheinlichkeit, dass bei 10 möglichen Ereignissen bis zu 2 (also 0,1 oder 2) auftreten, gleich P=0,9. Das ist gleichbedeutend mit Folgendem: In einer Urne seien 11,5% rote Kugeln und der Rest schwarze Kugeln. Man zieht 10 Kugeln. Die Wahrscheinlichkeit, bis zu 2 (also 0, 1 oder 2) rote gezogen zu haben, liegt bei 90%. |
| Bei einer Eintrittswahrscheinlichkeit eines einzelnen Ereignisses von p=0,449 ist die Wahrscheinlichkeit, dass bei 10 möglichen Ereignissen bis zu 2 (also 0,1 oder 2) auftreten, gleich P=0,1. Das ist gleichbedeutend mit Folgendem: In einer Urne seien 44,9% rote Kugeln und der Rest schwarze Kugeln. Man zieht 10 Kugeln. Die Wahrscheinlichkeit, bis zu 2 (also 0, 1 oder 2, demnach relativ wenige) rote gezogen zu haben, liegt bei 10%. |
Für die Eintragung in das Weibullnetz bedeutet das:
Wenn man bei der Ermittlung der Ausfallrate zu (100-10)% = 90 %sicher gehen will, dann trägt man den 2. von 10 Ausfällen bei der Wahrscheinlichkeit p=0,449 ein.
Reicht
dagegen 50/50 Sicherheit, dann trägt man
Für praktische Anwendung hierzu siehe Vertiefung unter Weibull Netz, jeweils bei "Ermitteln der Rangpositionen",
und zur Berechnung mittels Excel Solver diese Exceltabelle.
Siehe auch Likelihood Ratio und Fisher Matrix für weitere Methoden zur Berechnung von Vertrauensintervallen.