Anderson Darling Test mit Excel Beispiel
Der
Anderson Darling Test ist ein Anpassungstest
für verschiedene Verteilungsfunktionsarten.
Ein
modifizierter
Kolmogoroff Smirnoff Anpassungstest.
Während
letzterer auf jede Verteilungsfunktionsart ohne weitere Modifikation
angewendet werden kann, ist der Anderson Darling Test
verteilungsfunktions-spezifisch aufgebaut, das heisst, er funktioniert
beispielsweise bei Normalverteilung anders als bei Weibullverteilung.
Das
hat zur Folge, das
kritische Werte in Abhängigkeit von der Verteilungsfunktionsform
tabelliert werden müssen. Dafür ist er jedoch genauer.
Der
Anderson Darling Test bewertet die Randbereiche ("Schwänze")
von Verteilungsfunktionen kritischer als der Kolmogoroff
Smirnoff Anpassungstest.
Normalverteilung:
Die
Prüfgrösse und
kritischer Wert (zum
Signifikanzniveau 95%) des
Anderson Darling Tests lauten:
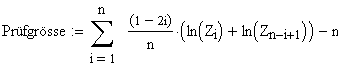
Die Prüfgrösse wird auch als A oder A2 bezeichnet
|
Die Werte i müssen
aufsteigend geordnet
sein.
n: Stichprobengrösse
Zi: Die kumulierte Fläche der
Normalverteilung von -00 bis zum Wert xi
|
Der
kritische Wert (Schwellenwert) hängt, abgesehen vom Alpharisiko, auch
von der Frage ab, ob Mittelwert und Standardabweichung als bekannt
vorausgesetzt werden können, oder ob sie aus den Messwerten geschätzt
werden müssen. Für Alpha = 5% und sowohl Mittelwert als auch
Standardabweichung bekannt, gilt
Kritischer_Wert0,95 = 0,752.
Wenn sowohl Mittelwert als auch Standardabweichung als unbekannt
vorausgesetzt werden, also aus den Messdaten geschätzt werden müssen, dann
gilt
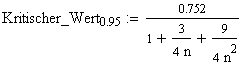
Hinweis: Anstelle den kritischen Wert umzuskalieren kann man auch die Prüfgrösse A in A*umskalieren:
A* = A(1+3/4n +9/4n2)
Für Alpha = 10% bzw. 1% nimmt man statt 0,752 den Wert 0,631 bzw. 1,035.
|
n:
Stichprobengrösse |
Bei Lognormal-verteilten
Daten muss man die
Daten zuerst logarithmus-transformieren, dann kann man mit dem Anderson
Darling Test für Normalverteilung fortfahren.
Für ein Berechnungsbeispiel (A-D Test auf Normalverteilung) in
Excel siehe hier.
Weibullverteilung:
Der
Anderson Darling Test auf Weibullverteilung funktioniert nahezu identisch.
Es wird dieselbe Prüfgrösse wie weiter oben berechnet. Die Formel ist identisch, doch sind die Zi dann die Quantile der Weibullverteilung, und werden daher anders berechnet als die Zi der Normalverteilung.
Die Schwellenwerte sind denen für Normalverteilung sehr ähnlich:
0,637 für alpha = 10%, 0,757 für 5% und 1,038 für 1%.
Der Anpassungsfaktor für den Fall unbekannter Verteilungsparameter bekommt die Gestalt
A* = A[1+1/(5n1/2)]
Für
eine Berechnungsbeispiel (A-D Test auf Weibullverteilung) in Excel siehe hier.
24.09.2018