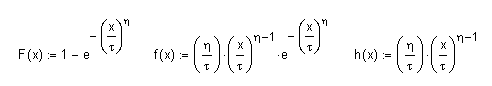
Ursprünglich von Waloddi Weibull eingeführte, in der Zuverlässigkeitstechnik sehr weit verbreitete Verteilungsfunktion.
Die Ausfallrate weibullverteilter Populationen folgt einem Potenzgesetz: h(x)= axb
Siehe Weibullanalyse.
Die Weibullverteilung hat in der Zuverlässigkeitstechnik -trotz ihrer hohen Bekanntheit- lediglich heuristischen Charakter, obgleich in der Extremwertstatistik die streng mathematische Rechtfertigung gefunden worden ist. ( Siehe Extremwert Theorem).
Die Weibullverteilung besitzt 2 oder 3 Parameter:
die charakteristische Lebensdauer t
den Formfaktor h
evtl. die zeitliche Verschiebung x0
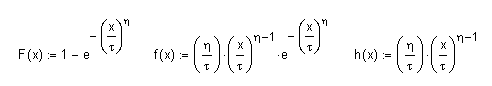
h: Formfaktor
t: Charakteristische Lebensdauer (Mittelwert)
F: Verteilungsfunktion, f: Dichtefunktion, h: Ausfallratenfunktion;
die Ausfallratenfunktion der Weibullverteilung hat also die Form h(x)= axb
| Erwartungswert | Varianz | Schiefe | Wölbung | Modalwert | Median | Bemerkungen |
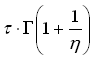 |
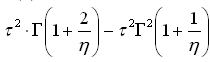 |
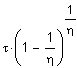 |
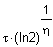 |
Γ(...): siehe Gammafunktion.
Mit dem Formfaktor h kann das Ausfallverhalten modelliert werden:
h=1 --> konstante Ausfallrate, Exponentialverteilung
h<1 --> abnehmende Ausfallrate (Burn In, Frühausfälle, praktisch nie kleiner als 0,5)
h>1 --> zunehmende Ausfallrate (Verschleiss, praktisch nie grösser als 10)
h=2 --> Rayleighverteilung, ähnlich Lognormalverteilung.
h= 3,5 --> annähernd Normalverteilung
Für eine anschauliche Darstellung der Weibullverteilung siehe das Tabellenblatt "Weibull" dieser Exceldatei.