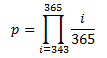Geburtstagsparadoxon

Ein Paradoxon.

Hinter dem Geburtstagsparadoxon verbirgt sich die Frage: Wie wahrscheinlich ist es, dass in einer Gruppe von 23 zufällig gewählten Menschen wenigstens 2 am selben Tag Geburtstag haben? 

Antwort: ca. 50%. 

Paradox ist hier lediglich, dass man bei unvoreingenommener Schätzung deutlich weniger als 50% annehmen würde. 

Man muss hier aber beachten, dass der Tag an sich keine Rolle spielt, sondern lediglich 2 Leute an irgendeinem der möglichen 365 Tage gemeinsam Geburtstag haben sollen. 

Berechnung: 

Man teilt den 23 Personen nacheinander Geburtstage zu in der Art, dass niemand am selben Tag Geburtstag hat. 

Die erste Person kann frei wählen. Die zweite Person ist bereits eingeschränkt: Die Wahrscheinlichkeit, dass sie an einem anderen Tag Geburtstag hat wie die erste Person, liegt bei 364/365. Für die dritte Person gilt entsprechend 363/365, für die vierte 362/365, usw. 

Die Wahrscheinlichkeit, dass von 23 Personen niemand am selben Tag Geburtstag hat, liegt also bei 

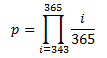=0.493.  

--> Die Wahrscheinlichkeit, dass wenigstens 2 Personen am selben Tag Geburtstag haben, liegt demnach bei (1-0.493) = 0.507.