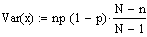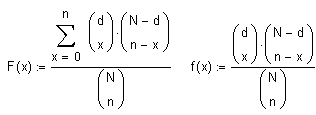
N: Grösse der Grundgesamtheit
d: Anzahl Merkmalsträger in der Grundgesamtheit
n: Grösse der Stichprobe
x: Anzahl Merkmalsträger in der Stichprobe
zurück zum Glossar (Hypergeometrische Verteilung)
Herleitung des Erwartungswertes der Hypergeometrischen Verteilung.
Die Hypergeometrische Verteilung F(x) sowie deren Dichtefunktion f(x) sind definiert zu:
|
|
N: Grösse der Grundgesamtheit d: Anzahl Merkmalsträger in der Grundgesamtheit n: Grösse der Stichprobe x: Anzahl Merkmalsträger in der Stichprobe |
Der Erwartungswert E(x) ergibt sich, wenn man alle in Frage kommenden Werte mit ihren zugehörigen Wahrscheinlichkeiten gewichtet aufaddiert.
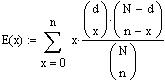
Nun
wendet man
folgende Beziehung auf den linken Teil des Zählers und den Nenner an: 
(Diese Beziehung kann man mittels explizitem Hinschreiben der im Binomialausdruck enthaltenen Fakultäten sehr leicht überprüfen)
Ausserdem kann man die Summe anstelle von 0 bis n auch von 1 bis n laufen lassen, da für x=0 ja lediglich 0 zum Erwartungswert addiert wird.
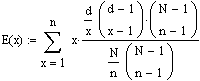Anmerkung: In der rechten Klammer des Zählers
muss es N-d statt N-1 heissen und n-x statt n-1.
Die beiden x ausserhalb der Binomialkoeffizienten kürzen sich heraus.
Umstellen des rechten Teils des Zählers führt zu:
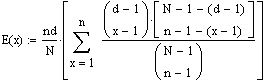
Als letzten Schritt ersetzt man die Laufvariable x durch y+1. y läuft dann von 0 bis n-1:
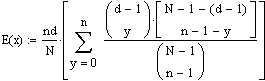
In der grossen Klammer steht nun wieder eine Hypergeometrische Verteilung F(y). Statt anfänglich x steht nun y, statt d steht d-1, statt N steht N-1, und statt n steht n-1. Somit muss die grosse Klammer = 1 ergeben, also:
Herleitung der Varianz der Hypergeometrischen Verteilung.
Die Hypergeometrische Verteilung F(x) sowie deren Dichtefunktion f(x) sind definiert zu:
|
|
N: Grösse der Grundgesamtheit d: Anzahl Merkmalsträger in der Grundgesamtheit n: Grösse der Stichprobe x: Anzahl Merkmalsträger in der Stichprobe |
Die Varianz ergibt sich zu
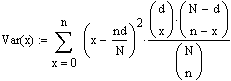(= das am Erwartungswert nd/N zentrierte zweite Moment. Siehe
zentrale
Momente)
Ausmultiplizieren ergibt:
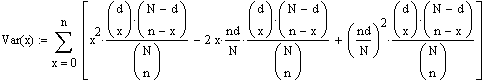
Der zweite Term in der Klammer ergibt 2nd/N *Erwartungswert (siehe oben, Herleitung des Erwartungswertes).
Der dritte Term in der Klammer ergibt (nd/N)2*1.
Zusammengefasst ergibt sich:
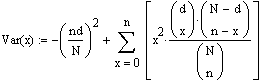
Nun
verwendet
man wieder die Eigenschaft (siehe oben),
lässt die Summe wieder von 1 bis n anstelle 0 bis n laufen (wie oben),
setzt anstelle d nun (d-1)+1 (wie oben) und
setzt statt n nun (n-1).
Man erhält wieder einen längeren Ausdruck, der an einer Stelle den Erwartungswert einer Hypergeometrischen Verteilung, und an einer anderen Stelle die Hypergeometrische Verteilung selbst enthält.
Ersteren vereinfacht man zu nd/N, und Letzteren zu 1.
Mit weiteren rein algebraischen Umformungsschritten gelangt man zu
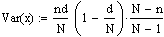
Mit p= d/N ergibt sich
