Die
Markov Methode kommt besonders dann zum Einsatz, wenn das System
Zustände oder Verhaltensweisen hat, die nicht eindeutig gut oder
schlecht sind.
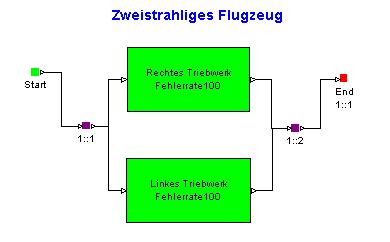
Vorweg: Das folgende Markov
Beispiel würde als Blockdiagramm so aussehen:
Obwohl es auf
den ersten Blick einfacher aussieht, hat es einen ganz entscheidenden
Nachteil. Mehr dazu im folgenden Markov Beispiel.
Markov Analyse
Auf Markov Ketten basierende Analysemethode von Systemen in der Zuverlässigkeitstechnik.
Konkurrierend mit Zuverlässigkeits-Blockdiagrammen.
Markov Ketten sind ein Spezialfall stochastischer Übergangsprozesse
Statistische Übergangsprozesse lassen sich wie folgt beschreiben:
![]()
Dies
bedeutet, dass die
Die Markov Eigenschaft ist nun wie folgt definiert:
![]()
Die Wahrscheinlichkeit, dass ein System im Zustand Xn+1 vorgefunden wird, hängt bei Markov Ketten allein vom unmittelbar zuvor eingenommenen Zustand Xn ab (= Markov Prozess).
Für die Antreffwahrscheinlichkeit des Systems in einem Zustand ist also einzig nur der zuvor eingenommene Zustand massgebend.
Gleichbedeutend damit ist die mathematische Eigenschaft, dass Übergangswahrscheinlichkeiten (oder -raten) zwischen je 2 Zuständen zeitlich konstant sein müssen, was wiederum gleichzusetzen ist damit, dass Übergänge zwischen Zuständen rein zufälliger Natur sind.
Folgendes Bild gibt ein Beispiel, aus dem auch ein Vorteil von Markov-Analysen gegenüber Blockdiagrammen hervorgeht.
Der Zustand "Beide Triebwerke ausgefallen, Flugzeug gleitet" kann nicht durch einen funktionalen Block dargestellt werden, sondern ist ein reiner Zustand.
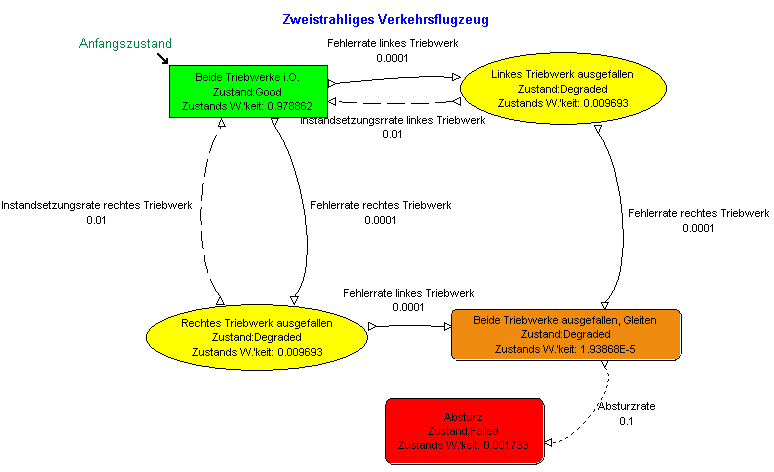
Die Markov Methode hat vor allem bei komplexeren Systemen sehr nützliche mathematische Eigenschaften.
Dies soll anhand des obigen Beispiels (zweistrahliges Flugzeug) erläutert werden.
1. Beschreibung der vorkommenden Zustände
| Zustandsnummer | Zustandsbeschreibung |
| 1 | Beide Triebwerke ok. |
| 2 | Triebwerk A ausgefallen, B ok. |
| 3 | Triebwerk B ausgefallen, A ok. |
| 4 | Beide Triebwerke ausgefallen. |
2. Festlegen der Übergangswahrscheinlichkeiten zwischen je 2 Zuständen.
| P1->1 =0,9 | P2->1 =0,8 | P3->1 = 0,8 | P4->1 =0 | |
| P1->2 =0,05 | P2->2 =0,1 | P3->2 = 0 | P4->2 =0,4 | |
| P1->3 =0,05 | P2->3 =0 | P3->3 = 0,1 | P4->3 =0,4 | |
| P1->4 =0, | P2->4 =0,1 | P3->4 = 0,1 | P4->4 =0,2 | |
| Summe | P1->irgendwo = 1,0 | P1->irgendwo = 1,0 | P1->irgendwo = 1,0 | P1->irgendwo = 1,0 |
Hier bedeutet P1->2 =0,04, dass, wenn sich das System im Zustand 1 befindet, es mit der Wahrscheinlichkeit von 0,04 innerhalb des Betrachtungszeitraums in den Zustand 2 begeben wird.
3. Matrixschreibweise.
|
Spaltennummern stehen für den Zustand vor dem Übergang.
Zeilennummern stehen für den Zustand nach dem Übergang. |
|
Offenbar steht an der Stelle Pxy die Übergangswahrscheinlichkeit des Systems vom Zustand x in den Zustand y während des Betrachtungszeitraumes.
Wenn das System im Zustand 1 ist, dann ergibt die Summe der ersten 3 Werte in Spalte 1 die Verfügbarkeit nach dem Betrachtungszeitraum an, und der letzte Wert in Spalte 1 die Nicht-Verfügbarkeit. Das liegt daran, weil nur der Zustand 4 als Fehlzustand deklariert worden ist und das System in den Zuständen 1,2 und 3 als intakt gilt.
Entsprechendes gilt für die restlichen Spalten.
Interessant wird es, wenn man nach der Verfügbarkeit des Systems nach 2 oder mehr (n) Betrachtungszeiträumen fragt.
Dies ergibt sich ganz einfach durch Potenzieren der Matrix mit n.
Im Folgenden sind die Ergebnismatrizen für n=2 und n=3 angegeben
| n=2: |
Rechenvorschrift, Beispiel:
|
n=3:
Auch hier gilt wieder:
Wenn das System im Zustand 1 ist, dann ergibt die Summe der ersten 3 Werte in Spalte 1 der Ergebnismatrizen die Verfügbarkeit nach 2 bzw. 3 Betrachtungszeiträumen an, und der letzte Wert in Spalte 1 die Nicht-Verfügbarkeit. Das liegt daran, weil nur der Zustand 4 als Fehlzustand deklariert worden ist.
Entsprechendes gilt für die restlichen Spalten.
Bei Betrachtung eines kontinuierlichen Zeitraumes stehen anstelle der Übergangswahrscheinlichkeiten dann Übergangsraten.
Mathematisch ändert sich im Prinzip nichts.
Die Übergangsraten von besseren Zuständen nach schlechteren Zuständen werden im Allgemeinen als Fehlerraten, die Übergangsraten in umgekehrte Richtung als Reparaturraten bezeichnet.
27.08.2005