Benford's Law, Benfords Gesetz
In
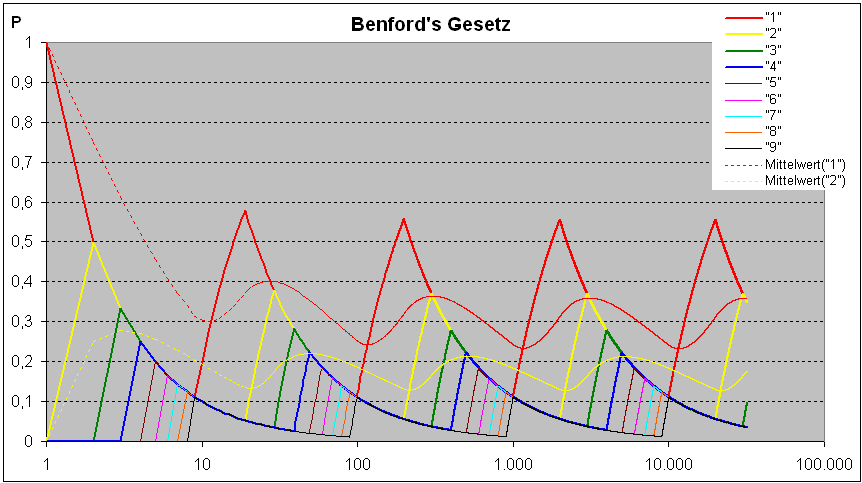
folgendem Bild wird Benford's Gesetz visualisiert. Erläuterungen folgen weiter unten.
Die x-Achse ist
logarithmisch. Die Auftretenswahrscheinlichkeiten der Anfangsziffern
haben sägezahnförmige Verläufe.

Das Benfordsche Gesetz besagt folgendes: Die führenden Ziffern von Zufallszahlen unterliegen folgender Häufigkeitsverteilung:
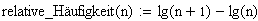
n
ist die jeweilige führende Ziffer, lg bedeutet Logarithmus
zur Basis
10.
Das
Benfordsche Gesetz ist in der Theorie nicht ganz einfach, weshalb hier
nur eine qualitative Erklärung versucht wird.
Ausserdem
sind die Anforderungen des Benfordschen
Gesetzes an das zugrunde liegende
Zahlenmaterial recht hoch:
Letzteres
bedeutet nicht, dass es sich um Zufallszahlen handeln muss, im
Gegenteil: Nicht die Zahlen selbst sind zufällig (dann wären sie ja
gleichverteilt), sondern die Prozesse, durch die sie zustandegekommen
sind. Solche Prozesse ergeben immer eine Häufung der Zahlen am unteren
Ende des möglichen Wertebereiches.
In konkreten Werten sieht das Benfordsche Gesetz so aus:
| Führende Ziffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| relative Häufigkeit [%] | 30.1 | 17.6 | 12.5 | 9.7 | 7.9 | 6.7 | 5.8 | 5.1 | 4.6 |
Zahlenbeispiele
1.5E+2 6.81E 0 2.223E-3 3E-6
Letztere Zahl könnte man auch 0.3E-5 schreiben, dann wird aber die führende Ziffer (hier 3) nicht deutlich.
Entscheidend ist, dass
nicht die Anfangsziffern der Zahlen (diese hängen ja von der Schreibweise ab), sondern die führenden Ziffern gemeint sind.
was man am besten sieht, wenn man die Zahlen in wissenschaftlicher Notation schreibt.
Man sieht dann auch, dass die Null keine führende Ziffer sein kann.
"natürliches" Zahlenmaterial in praktisch allen realen Fällen logarithmisch verteilt ist.
Die Logarithmen von natürlichem Zahlenmaterial sind also gleichverteilt.
In der Natur sind logarithmische Skalen der Normalfall. Fast die gesamte menschliche Sinneswahrnehmung funktioniert logarithmisch (Sehen, Hören, Fühlen).
Das
Problem ist lediglich, dass dies nicht unserem gewohnten Zahlenweltbild
entspricht.
Da
unser Zahlensystem die Basis 10 hat, braucht man sich auch nicht zu
wundern, dass der für das Benfordsche Gesetz zutreffende Logarithmus
ausgerechnet der Zehnerlogarithmus ist.
Betrachtet man z.B. die Zahlen von 1 bis 1000, dann deckt der Bereich von 100 - 199 einen relativen Grössenbereich von Faktor 199/100~2~ 100% ab, der Bereich von 900 -999 dagegen nur einen Faktor von 999/900 ~ 1.11~11%
Nach dieser anschaulichen Einfachbetrachtung sollte in "natürlichem" Datenmaterial die 1 als führende Ziffer etwa neunmal häufiger vorkommen als die 9, was nach obenstehender Tabelle zumindest nicht ganz falsch ist (30.1/4.6 =6.5).
Anderer Denkansatz: Wenn man die ganzen Zahlen von 1 bis n hochzählt, und bei n aufhört, dann sind die Anfangsziffern für folgende n gleichverteilt: 9, 99, 999, 9999, usw.
Hört man dagegen bei beliebigem n auf zu zählen, dann ist die 1 nie benachteiligt, die 2 nur selten,.... und die 9 immer.
Nochmalige Betrachtung des Benfordschen Gesetzes:
Die Lösung der Gleichung x=lg(n) lautet für die Ziffern n=1...9:
| Ziffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| x = | 0 | 0.301 | 0.477 | 0.602 | 0.699 | 0.778 | 0.845 | 0.903 | 0.954 |
Die Wahrscheinlichkeit, mit der die 1 als führende Ziffer auftaucht berechnet man zu 0.301-0 =30.1%.
Für die Ziffer 2 ergibt sich 0.477-0.301 = 17.6%
usw.