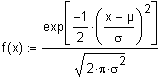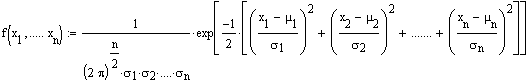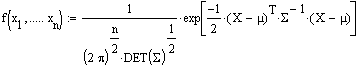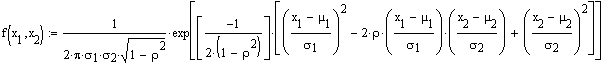Mehrdimensionale
Normalverteilung
Da die mehrdimensionale Normalverteilung ebenso wie
die
Normalverteilung nicht geschlossen darstellbar ist, wird hier die
Dichtefunktion angegeben:
Für den Fall abhängiger xi nimmt die
n-dimensionale Normalverteilung folgende Gestalt an:
(Ab hier kommt man ohne Matrixnotation
nicht
mehr aus, weil die konventionelle Darstellung für jedes n anders
aussehen würde.
Eine Anleitung zum Rechnen mit Matrizen
wird
unter der Rubrik "
Multiple lineare Regression" mitgegeben)
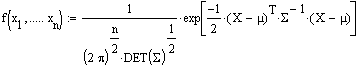 |
Es bedeuten:
S: Varianz-Kovarianzmatrix der unabhängigen Variablen xi (n-dimensionale
Matrix).
S-1: Inverse Matrix zu S (ein verallgemeinerter Kehrwert)
DET (...) Determinante von (...)
X: Vektor der unabhängigen Variablen xi
µ: Mittelwertsvektor
(...)T Die Transponierte von (...)
|
Für den zweidimensionalen Fall sieht das in
konventioneller Darstellung wie folgt aus:
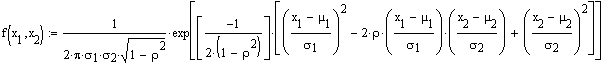
Der mittlere Term im Exponenten entspricht der
Kovarianz
der beiden unbhängigen Variablen x1 und x2.
Der Nenner im Vorfaktor (ohne 2p)
ist die Wurzel der Determinante der (in diesem Fall 2x2-dimensionalen)
Varianz-Kovarianzmatrix.
Man erkennt leicht, dass für r
= 0 die ganz oben angegebene Formel für unabhängige x1 und x2
(n=2) herauskommt.
Im dreidimensionalen Koordinatensystem ergibt sich mit
r = 0 eine um die z- Achse
rotationssymmetrische
Glockenform.
Ähnlich wie im eindimensionalen Fall beschreibt die
Dichtefunktion der n-dimensionalen Normalverteilung eine n-dimensionale
Glockenform.
Für das Aussehen der Glockenform ist es von
entscheidender Bedeutung, welche Werte die
Korrelationskoeffizienten der unabhängigen Variablen xi annehmen.
Die "runde" Glockenform ergibt sich nur, wenn alle
Korrelationskoeffizienten = 0 sind.
Was bei r ungleich 0
passiert, sieht man am Besten im zweidimensionalen Fall.
Bei r = 1 sind beide
Dimensionen streng korreliert und man erhält eine eindimensionale
Glockenform, die sich im 45 Grad Winkel über die beiden ursprünglichen
Dimensionen erstreckt.
Bei Werten von r zwischen
0 und 1 ergibt sich eine elliptische Glockenform.