Orthogonale Felder für Design of Experiments und Taguchi

In der statistischen Versuchsplanung sind orthogonale Felder die tabellarische Visualisierung der bei den Versuchen einzustellenden Faktorstufen.

Eine n x m Matrix, deren Elemente folgende Eigenschaften besitzen:

• Jeder Spalte der Matrix wird eine Menge an möglichen Symbolen zugewiesen, derer sich die Spaltenpositionen bedienen können. 

• Vergleicht man zeilengleiche Positionen irgendwelcher Spaltengruppen, dann kommt jede Symbolkombination innerhalb einer Spaltengruppe genau gleich oft vor.  

Spezielle von Taguchi entworfene orthogonale Felder gibt es hier.

Mathematisch bedeutet Orthogonalität lineare Unabhängigkeit.

Folgend ein nicht ganz triviales Beispiel, da es unterschiedliche Stufenzahlen enthält: 

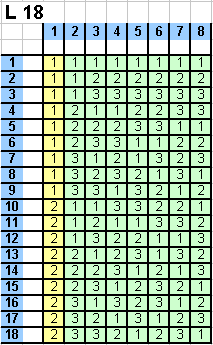Links ist beispielhaft das Taguchi  L18 Feld dargestellt.  1 Faktor mit 2 Stufen und 7 Faktoren mit 3 Stufen.   Dieses Feld würde man also heranziehen, wenn man einen Versuch plante, bei dem ein Merkmal (=Faktor) auf 2, und bis zu 7 Merkmale auf bis zu 3 Stufen gemessen würden. Man erkennt: Spalten 1 und 2:      Jede Kombination (11,12,13,21,22,23) kommt in genau 3 Zeilen vor.  Spalten 1 und 3:      Jede Kombination (11,12,13,21,22,23,31,32,33) kommt in genau 3 Zeilen vor.  Spalten 2 und 3:      Jede Kombination (11,12,13,21,22,23,31,32,33) kommt in genau 2 Zeilen vor.  Ähnliches gilt für alle übrigen Spaltenpaare.

In diesem Beispiel funktioniert es nur für Spaltenpaare. 

Felder, bei denen dies auch für Spalten-tripletts, -quartetts, usw. gilt, sind deutlich umfangreicher. 

Als Grenzfall ergibt sich eine Permutationstabelle, in der jede denkbare Gesamtzeilenkombination genau einmal vorkommt (--> Vollfaktorieller Versuchsplan). 

Der zu dem genannten Beispiel passende vollfaktorielle Versuchsplan hätte 2¹*3⁷ = 4374 Zeilen. 

Mit dem vollfaktoriellen Versuchsplan liessen sich alle Haupteffekte und Wechselwirkungseffekte sicher analysieren. Mit dem links beschriebenen Beispiel ("nur Spaltenpaare") lassen sich lediglich Haupteffekte analysieren; bereits die Wechselwirkungen erster Ordnung sind mit den Haupteffekten vermischt.