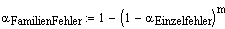 ,
was für grosse m gegen 1 konvergiert. (Alpha Inflation)
,
was für grosse m gegen 1 konvergiert. (Alpha Inflation)
Bei mehrfachen oder multiplen
Tests besteht das Problem der Alpha Inflation, denn häufiges Testen
führt irgendwann zwangsläufig zu Signifikanz.
Abhilfe schafft hier z.B. das Hochsetzen der Schwelle für Signifikanz,
die Alpha Adjustierung.
zurück zum Glossar (Bonferroni)
Bonferroni Ansatz
Anpassung des Signifikanzniveaus bei multiplem Testen.
Testete
man ohne Korrektur m Hypothesen, oder die selbe Hypothese an m Stichproben,
so würde man bei gegebenem Alpha
Risiko mit der folgenden
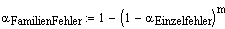 ,
was für grosse m gegen 1 konvergiert. (Alpha Inflation)
,
was für grosse m gegen 1 konvergiert. (Alpha Inflation)
1. Bonferroni-Ansatz:
"Hochschrauben
des Signifikanzniveaus bzw. Herabsetzen des Alpha Risikos auf alphaHerabgesetzt
= alpha
Beispiel:
alpha
Mit den neuen 2% kommt die neue
Das ist ein klein wenig zu konservativ. Ausserdem werden tatsächliche Unterschiede schwerer erkannt:
Alpha Inflation ---> Beta Deflation.
2. Bonferroni-Holm-Ansatz (Sequentieller Bonferroni Ansatz):
zyklisch den vorhergehenden Schritt fortsetzen bis keine Signifikanzen mehr gefunden werden.
3. Duncan: Unabhängige Hypothesen
Die Einzelfehlerwahrscheinlichkeit
Danach berechnet
Beispiel:
Wenn man die Einzelfehlerwahrscheinlichkeit auf 2,085% festlegt und 5 Stichproben zu testen sind, dann liegt die Familienfehlerwahrscheinlichkeit bei 1-(1-0,02085)5 = genau 10%.
Siehe auch Post Hoc Tests.
zurück zum Glossar (Bonferroni)