Geometrische Verteilung Bernoulliverteilung

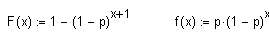
Die geometrische Verteilung kann man als Wartezeit-Verteilung bis zum ersten Ereignis auffassen.

Es ist die Wahrscheinlichkeitsverteilung dafür, dass das gewünschte Ereignis bei einem wiederholten Bernoulli Experiment nach genau x Wiederholungen zum ersten Mal eintritt.

Die geometrische Verteilung ist daher ein Spezialfall der negativen Binomialverteilung für r=1.

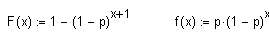
Erwartungswert: E(x)= (1-p)/p   Varianz: Var(x)= (1-p)/p² 

p: Eintrittswahrscheinlichkeit des gewünschten Ereignisses bei einer Durchführung des Bernoulli Experiments.

F: Verteilungsfunktion, f: Dichtefunktion

Für eine Auflistung der Wechselbeziehungen einiger wichtiger Verteilungsfunktionen siehe hier.