Logit Probit Normit Modell
Heuristisches mathematisches Modell zur Beschreibung des gerichteten Zusammenhangs einer dichotomen abhängigen Variablen in Abhängigkeit von einer wenigstens nominalskalierten unabhängigen Variablen.
Spezialfall des log-linearen Modells.
Beispiel:
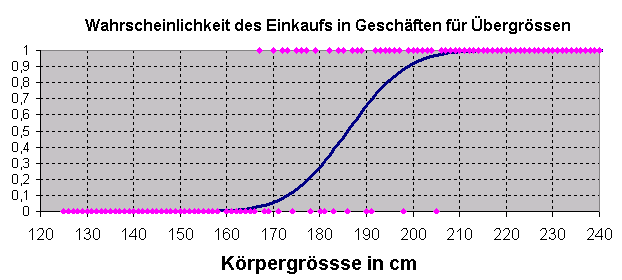
Es soll ein formaler Zusammenhang hergestellt werden zwischen der Körpergrösse von Menschen und deren Kaufverhalten bezüglich Übergrössen.
Pauschal lässt sich vermuten, dass Menschen umso wahrscheinlicher in Geschäften für Übergrössen einkaufen, je grösser deren Körpergrösse ist.
Befragte man eine grössere Anzahl Menschen nach deren Neigung zu Geschäften mit Übergrössen (ja = 1; nein = 0)
berechnet
daraus die

Die rosa Punkte sind die einzelnen Messwerte, die blaue Kurve ist die bestangepasste kumulierte Wahrscheinlichkeitsverteilung.
Zur Modellierung der S-Kurve (blau) werden meistens folgende, so genannte Link Funktionen herangezogen:
logistische Verteilung ---> Logit Modell
wegen des formalen Zusammenhangs der logistischen Verteilungsfunktion zum Odds Ratio, siehe auch unter logistische Verteilung.
weil damit leichter zu rechnen ist
Modellgleichung: 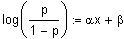
Normalverteilung ---> Probit oder Normit Modell.
Die Normalverteilungsfunktion ist in der Gegend ihres Wendepunktes steiler als die logistische Verteilungsfunktion.
Das Ergebnis einer Logit (Probit, Normit) Analyse ist eine bestangepasste Kurve, die zu Vorhersagezwecken herangezogen werden kann.
Ähnlich wie die lineare Regression die beste Anpassung einer Geraden an eine Punktewolke darstellt, ist die logistische Regression eine beste Anpassung der logistischen Funktion an die beiden "Punktewolken" der dichotomen abhängigen Variablen.
Die abhängige Variable kann ja nur 2 Zustände einnehmen, weshalb die Punkte sich nur auf die beiden horizontalen Achsen "Wahrscheinlichkeit =0" und "Wahrscheinlichkeit =1" verteilen.