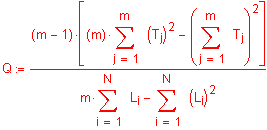
Cochran Q-Test mit Excel Beispiel
Der Cochran Q-Test ist ein parameterfreies Testverfahren, mit dem festgestellt werden soll, ob zwei oder mehr abhängige Stichproben signifikant im Anteil der Fälle in jeder von zwei Kategorien differieren.
Erweiterung des Mc Nemar Tests auf mehr als 2 Zeitpunkte UND dichotomer unabhängiger Variable.
Nominales, dichotomes Skalenniveau.
Die Prüfgrösse ist Chi Quadrat verteilt mit f= (m-1) Freiheitsgraden, wobei m die Anzahl der Messzeitpunkte ist.
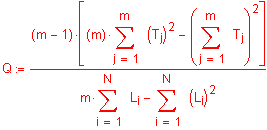
m: Anzahl Messzeitpunkte
Tj: Anzahl Messobjekte, die beim Zeitpunkt j das Merkmal aufweisen (Spaltensumme)
N: Anzahl aller Testobjekte
Li: Anzahl Messzeitpunkte, an denen das Testobjekt i das Merkmal aufweisst (Zeilensumme)
Beispiel Cochran Q-Test: Wirkung eines Werbespots auf Testpersonen nach wiederholten Sendungen.
1.) Originaldaten:
+ = Zuneigung, - = Ablehnung
| Testperson Nr. | Zuneigung / Ablehnung nach Wiederholung des Werbespots | Es hat den Anschein, dass der Spot nach mehrmaliger Wiederholung eher angenommen wird. | ||||
| 1 | 2 | 3 | 4 | |
||
| 1 | - | - | - | + | + | |
| 2 | + | - | - | + | - | |
| 3 | - | + | + | + | + | |
| 4 | + | + | - | - | - | |
| 5 | + | - | - | + | + | |
| 6 | - | - | - | - | + | |
| 7 | - | + | - | + | + | |
2.) Berechnung der Prüfgrösse.
Zeilensummen Li (Anzahl "+"): 2,2,4,2,3,1,3
Spaltensummen
Tj
Anzahl Freiheitsgrade: f =5-1 = 4
Q= 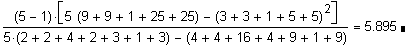
--> das Alpha Risiko beträgt 20.7 % bzw. das Signifikanzniveau 79.3%.
Die Nullhypothese kann also zum Alpha Risiko von 90% nicht verworfen werden.
Anmerkung zu diesem Beispiel:
Wäre das Datenmaterial so beschaffen, dass man die Nullhypothese z.B. zum Alpha Risiko von 90% verwerfen müsste, dann könnte man daraus nicht schliessen, dass der Werbespot einen positiven Trend im Zuschauerverhalten bewirkt. Es könnte auch beispielsweise sein, dass der Spot zuerst erfolgreich ist, dann dessen Wirkung jedoch ins Gegenteil umschlägt.
Der Q-Test prüft ja nur die Homogenität der Zeilen und Spalten, und nicht etwa einen Trend.
Für
eine Berechnung des Chi Quadrat Tests in
Excel siehe das Tabellenblatt