Bei Stress-Strength oder
Belastung-Belastbarkeitsdiagrammen geht es um Dimensionierung von
Sicherheitsreserven. Oft geht es um Bruchgrenzen.
zurück zum Glossar (Belastung - Belastbarkeit)
Belastung-Belastbarkeit oder auf englisch Stress-Strength
Gegenüberstellung von Belastungsverteilung und Belastbarkeitsverteilung.
Ergebnis ist die Wahrscheinlichkeit, mit der ein Individuum einer Population eine einmalige Belastung schadlos überstehen wird.
Überall in der Technik werden Teile bemasst mit dem Zweck, eine bestimmte Funktion für eine geplante Zeitdauer fehlerfrei zu erfüllen.
In der Realität sind Masse oder Eigenschaften irgendwie verteilt; sie streuen um einen bestimmten Wert.
Damit verbunden ist eine maximal mögliche Belastbarkeit, welche um einen bestimmten Wert streut.
Dem gegenüber steht eine irgendwie verteilte Belastung, die ihrerseits wieder um einen bestimmten Wert streut.
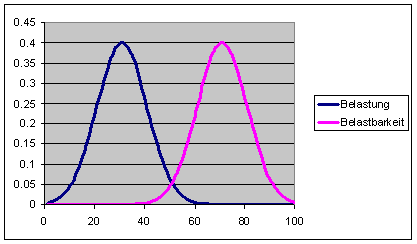
Im Idealfall widerstehen die weniger belastbaren Exemplare der grössten denkbaren Belastung, das heisst, die Verteilungsdichtefunktionen "Belastung" und "Belastbarkeit" überlappen sich nicht.
Wenn die beiden Verteilungsdichtefunktionen "Belastung" und "Belastbarkeit" sich jedoch überlappen, dann kommt es zu Ausfällen infolge zu grosser Belastung.
Wenn diesem Sachverhalt in wirtschaftlich vertretbarem Ausmass Rechnung getragen werden soll, dann ist die Kenntnis dieser beiden Verteilungsfunktionen notwendige Vorausetzung.
Folgendes
Bild zeigt aus Anschaulichkeitsgründen die beiden

Die
Zuverlässigkeit der gegebenen Belastungs-Belastbarkeitskonstellation
erhält man, indem man fragt, wie wahrscheinlich die Belastbarkeit
grösser
Mathematisch berechnet man die Zuverlässigkeit durch eine Doppelsumme bzw. Doppelintegral.
| Diskreter Fall | Kontinuierlicher Fall |
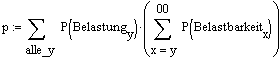 |
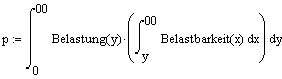 |
Erklärung des diskreten Falles:
Man
hält einen Punkt der Belastungskurve fest und multipliziert dessen
Dies macht man mit allen Punkten der Belastungskurve (äussere Summe, alle y).
Der kontinuierliche Fall funktioniert analog.
Wenn Belastung und Belastbarkeit normalverteilt sind mit den folgenden Mittelwerten und Standardabweichungen
![]() ,
,
dann ergibt sich für die Zuverlässigkeit p
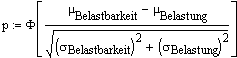 |
F: Verteilungsfunktion der Normalverteilung
(nicht geschlossen darstellbar)
Man erhält die linksstehende Gleichung ohne explizites Lösen der Integrale, sondern rein durch rechnerische Eigenschaften von F. |
Der Ausdruck innerhalb der Klammern wird auch als Sicherheitsabstand bezeichnet.
Anmerkungen:
Das zuvor Berechnete bezieht sich auf einen einmaligen (zufälligen) Belastungsvorgang.
Bei n Belastungen beträgt die Zuverlässigkeit pn.
Weiterhin wird davon ausgegangen, dass die Belastbarkeit sich mit der Anzahl erlebter Belastungen nicht ändert.
Meisstens ist es aber so, dass
Der Mittelwert der Belastungsverteilungsdichtefunktion mit der Anzahl Belastungen kleiner wird,
Die Standardabweichung der Belastungsverteilungsdichtefunktion mit der Anzahl Belastungen grösser wird.
In solchen Fällen kommt man meisstens nur noch mit Simulationsmethoden zu brauchbaren Ergebnissen.
Regel von Miner. Die folgende Punktschätzung gilt für Belastungen oberhalb der Ermüdungsgrenze, also in dem Bereich, wo tatsächlich eine Alterung stattfindet.
|
|
ni: Anzahl der Belastungen auf einem festen Belastungsniveau Ni: Medianwert der Anzahl Belastungen bis zum Ausfall auf diesem Belastungsniveau. Der Summenausdruck ist eine Summe aus Wahrscheinlichkeiten |
|
Beispiel: Die Medianwerte für die Anzahl Belastungen eines Gerätes auf den Belastungsniveaus 1,2 und 3 bis zum Ausfall seien N1=100.000, N2=60.000 und N3=30.000. Das Gerät wird 40.000 mal auf Niveau 1, 18.000 Mal auf Niveau 2 und 6.000 Mal auf Niveau 3 belastet.
Das Gerät wird die genannten Belastungen aller Voraussicht nach bestehen (weil 0.9<1) |
|
Derating: In der elektronischen Zuverlässigkeitstechnik ist Derating sehr verbreitet.
zurück zum Glossar (Belastung - Belastbarkeit)