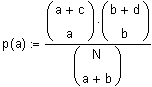 ,
, zurück zum Glossar (Fisher)
Exaktes Testpendant zum Vierfelder Chi Quadrat Test.
Beispiel
Es soll anhand einer Blitzumfrage die Nullhypothese überprüft werden, dass Frauen und Männer mit ihrem Körpergewicht gleichermassen zufrieden sind.
"Beide Geschlechter sind mit ihrem Körpergewicht gleichermassen zufrieden".
1.)
Originaldaten
| Zufrieden | Nicht zufrieden | |
| Frauen | 4 | 1 |
| Männer | 3 | 7 |
Offensichtlich ist die Voraussetzung, dass 80% aller Besetzungszahlen >5 sind, nicht erfüllt. Deshalb ist der exakte Test dem Chi Quadrat Test vorzuziehen.
2.)
Ermittlung der Randhäufigkeiten
| Zufrieden | Nicht zufrieden | Gesamt | |
| Frauen | 4 | 1 | 5 |
| Männer | 3 | 7 | 10 |
| Gesamt | 7 | 8 | 15 |
3.)
Bestimmung der Punktwahrscheinlichkeit [p(a)] genau der vorliegenden Konstellation.
Dazu wird die hypergeometrische Verteilung benötigt.
| Zufrieden | Nicht zufrieden | Gesamt |
Analogon zum Ziehen von Kugeln aus einer Urne:
B1 rote und B2 schwarze Kugeln in der Urne. Es werden N1 Kugeln ohne Zurücklegen gezogen. Wie gross ist die Punktwahrscheinlichkeit dafür, genau a rote Kugeln zu ziehen? |
|
| Frauen | a | b | N1 | |
| Männer | c | d | N2 | |
| Gesamt | B1 | B2 | N |
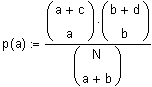 ,
,
eine äquivalente Darstellung lautet: 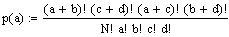
B1+B2=N: Grösse der Grundgesamtheit (Hier: Menge aller Kugeln)
B1=a+c: Anzahl Merkmalsträger in der Grundgesamtheit (Hier: Alle rote Kugeln)
N1=a+b: Grösse der Stichprobe (Hier: N1 gezogene Kugeln)
a: Anzahl Merkmalsträger in der Stichprobe (Hier: a rote Kugeln)
Mit der Excelfunktion HYPERGEOMVERT(a;N1;B1;N) = HYPERGEOMVERT(4;5;7;15) erhält man p(a=4) = 0,0932.
Mit einer Wahrscheinlichkeit von 9,32% würde man durch reinen Zufall also genau 4 rote Kugeln ziehen, wenn man 5 Ziehungen gemacht hätte und 7 rote und 8 schwarze Kugeln in der Urne wären.
Auf das Beispiel übertragen ist das so zu verstehen:
In einem Raum sind 15 Leute, 7 davon sind mit ihrem Körpergewicht zufrieden, 8 nicht. Nun wählt man 5 Leute zufällig davon aus.
Man hat jetzt 2 Gruppen: Eine besteht aus 5 Leuten, die andere aus 10 Leuten.
Die Wahrscheinlichkeit, dass in der 5er-Gruppe genau 4 Zufriedene sind, beträgt bei den gegebenen Daten 9,32%.
Interessant ist, dass die Attribute "Mann" und "Frau" bei dieser Betrachtungsweise gar nicht explizit auftauchen. Es ist lediglich von "2 Gruppen" die Rede.
4.)
Berechnung der Punktwahrscheinlichkeit aller "extremeren" als die vorliegende "Ziehung".
Im Beispiel waren von 5 "gezogenen Frauen" 4 zufrieden.
Das in diesem Beispiel einzige noch extremere Ereignis wäre, dass alle 5 Frauen zufrieden wären.
Die entsprechenden Besetzungszahlen sähen dann so aus:
| Zufrieden | Nicht zufrieden | Gesamt | |
| Frauen | 5 | 0 | 5 |
| Männer | 2 | 8 | 10 |
| Gesamt | 7 | 8 | 15 |
Mit der Excelfunktion HYPERGEOMVERT erhält man nun p(a=5)= 0,007
Die Summenwahrscheinlichkeit für die vorliegende Konstellation plus alle noch extremeren Konstellationen liegt also bei 0,0932+0,007=0,102, was einem Signifikanzniveau von 89,8% entspricht.
Forderten wir also 90 % Signifikanz, dann könnten wir im vorliegenden Fall die Nullhypothese "Beide Geschlechter sind mit ihrem Körpergewicht gleichermassen zufrieden", nicht ablehnen.
Für eine Reproduktion des Fisher exakten Testes in Excel siehe hier.
zurück zum Glossar (Fisher)
24.08.2005
zurück zum Glossar (Freeman Halton)
Erweiterung von Fisher's exaktem Test (2x2) auf k dichotome Stichproben (kx2).
Die Vorgehensweise ist ganz analog zu Fisher's exaktem Test, nur viel rechenintensiver.
Beispiel
Es soll anhand einer Blitzumfrage die Nullhypothese überprüft werden, dass Frauen, Männer und Kinder mit ihrem Körpergewicht gleichermassen zufrieden sind.
"Alle 3 Gruppen sind mit ihrem äusseren Aussehen gleichermassen zufrieden".
1.) Originaldaten
| Zufrieden | Nicht zufrieden | |
| Frauen | 4 | 1 |
| Männer | 3 | 7 |
| Kinder | 0 | 6 |
2.)
Ermittlung der Randhäufigkeiten
| Zufrieden | Nicht zufrieden | Gesamt | |
| Frauen | 4 | 1 | 5 |
| Männer | 3 | 7 | 10 |
| Kinder | 0 | 6 | 6 |
| Gesamt | 7 | 14 | 21 |
3.)
Bestimmung der Punktwahrscheinlichkeiten [p(a)] aller Kombinationen, bei denen die Randsummen (also Spaltensummen (7 und 14) und Zeilensummen (5, 10 und 6)) dem vorliegenden Ergebnis entsprechen.
Dies ist sicherer als sich von vorne herein nur auf die "noch extremeren" Kombinationen zu beschränken, da man sich schon bei 2x3 Feldern sehr leicht vertut.
Die Punktwahrscheinlichkeit für eine gegebene Kombination lautet in Erweiterung der Formel bei Fisher's exaktem Test:
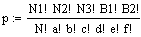 ,
,
wobei folgende Struktur zugrundegelegt worden ist.
| a | b | N1 |
| c | d | N2 |
| e | f | N3 |
| B1 | B2 | N |
Nach etwas mühsamem Suchen kommt man auf folgende 32 mögliche Kombinationen unter Beibehaltung aller Randsummen.
Die tatsächlich vorliegende Kombination ist gelb unterlegt.
| 5 | 0 | 5 | 0 | 5 | 0 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 3 | 2 |
| 2 | 8 | 1 | 9 | 0 | 10 | 3 | 7 | 2 | 8 | 1 | 9 | 0 | 10 | 4 | 6 |
| 0 | 6 | 1 | 5 | 2 | 4 | 0 | 6 | 1 | 5 | 2 | 4 | 3 | 3 | 0 | 6 |
| 3 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 |
| 3 | 7 | 2 | 8 | 1 | 9 | 0 | 10 | 0 | 10 | 1 | 9 | 2 | 8 | 3 | 7 |
| 1 | 5 | 2 | 4 | 3 | 3 | 4 | 2 | 5 | 1 | 4 | 2 | 3 | 3 | 2 | 4 |
| 2 | 3 | 2 | 3 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 |
| 4 | 6 | 5 | 5 | 6 | 4 | 5 | 5 | 4 | 6 | 3 | 7 | 2 | 8 | 1 | 9 |
| 1 | 5 | 0 | 6 | 0 | 6 | 1 | 5 | 2 | 4 | 3 | 3 | 4 | 2 | 5 | 1 |
| 1 | 4 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 |
| 0 | 10 | 7 | 3 | 6 | 4 | 5 | 5 | 4 | 6 | 3 | 7 | 2 | 8 | 1 | 9 |
| 6 | 0 | 0 | 6 | 1 | 5 | 2 | 4 | 3 | 3 | 4 | 2 | 5 | 1 | 6 | 0 |
Die zugehörigen Ergebnisse lauten:

Hierin sind alle selteneren Kombinationen als die Vorliegende grün hervorgehoben.
Die Summenwahrscheinlichkeit für die vorliegende plus aller noch selteneren Kombinationen beträgt
1,49%.
--> Die Nullhypothese
"Alle 3 Gruppen sind mit ihrem äusseren Aussehen gleichermassen zufrieden"
kann zum Signifikanzniveau von 95% nicht gehalten werden, zum Signifikanzniveau von 99% jedoch schon.
Für eine Exceltabelle des Freeman-Halton Testes für diverse Tafeln siehe hier.
zurück zum Glossar (Freeman Halton)
24.08.2005