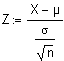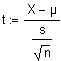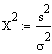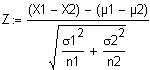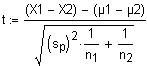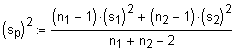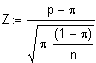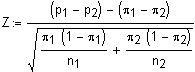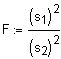Unter transformierten Statistiken versteht man umgeformte Ausdrücke, die auf folgende Verteilungsfunktionen Bezug nehmen:
Insbesondere die ersten 3 davon sind "künstlich geschaffene" Verteilungsfunktionen.
Zweck der genannten Verteilungsfunktionen ist nämlich weniger die Beschreibung von Wahrscheinlichkeitsverteilungen realer Grundgesamtheiten als vielmehr die Bestimmung von Vertrauensbereichen und Zufallsstreubereichen von Parametern.
Bei nahezu allen parametrischen Tests werden Prüfgrössen berechnet, die sich mittels der zuvor genannten Verteilungsfunktionen darstellen lassen.
Beispiele
| Erklärung | Erwartungswert / wenn gilt / Anzahl Freiheitsgrade | Transformierte Statistik |
| Vergleich
eines
Stichprobenmittelwertes mit dem einer normalverteilten Grundgesamtheit
(s bekannt) |
0 / X=µ / keine |
|
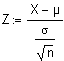
| Vergleich
eines
Stichprobenmittelwertes mit dem einer normalverteilten Grundgesamtheit
(s unbekannt) Siehe auch t-Verteilung. |
0 / X=µ / n-1 |
|
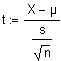
| Vergleich
einer
Stichprobenstreuung mit der Streuung einer normalverteilten
Grundgesamtheit
(s bekannt) Siehe auch Chi Quadrat Verteilung. |
1 / s=s / n-1 |
|
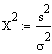
| ergleich des Unterschiedes zweier Mittelwerte X1 und X2 mit denen zweier vorgegebener Grundgesamtheiten mit jeweils bekannten Varianzen s12 und s22 . | 0 / X1-X2 = µ1-µ2 / keine |
 |
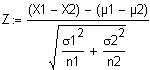| Vergleich
des Unterschiedes
zweier Mittelwerte X1 und X2 mit denen zweier
vorgegebener Grundgesamtheiten mit jeweils unbekannten Varianzen
s12 und s22
Siehe auch t-Verteilung. |
0 / X1-X2 = µ1-µ2 / n1+n2-2 |
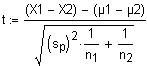
wobei
|
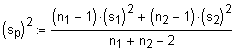
| Vergleich des Anteilswertes einer Stichprobe mit dem Anteilswert einer binomialverteilten bekannten Grundgesamtheit mit Mittelwert n*p und Varianz n*p (1-p) Siehe auch Standardnormalverteilung | 0 / p = p / keine |
 |
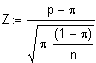| Vergleich des Unterschiedes zweier Anteilswerte mit dem Unterschied der Anteilswerte zweier binomialverteilter bekannter Grundgesamtheiten. | 0 / p1 = p1 und p2 = p2 / keine |
 |
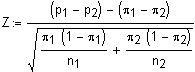| Vergleich des Unterschiedes zweier Varianzen s12 und s22 Siehe auch F-Verteilung | 1 / s1=s2 / n1-1 und n2-1 |
 |
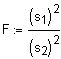