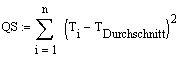
Kendalls Konkordanzkoeffizient für Urteilsübereinstimmung

Darf nicht mit Kendalls Tau verwechselt werden.

Dieses Korrelationsmass wurde entwickelt zur Beschreibung der Urteilsübereinstimmung bei ordinalem Skalenniveau. 

Der Wertebereich erstreckt sich von 0 (maximale Nicht-Übereinstimmung, Diskordanz) bis 1 (maximale Übereinstimmung, Konkordanz).

Siehe auch Cohen's und Fleiss' Kappa.

Hintergrund: 

m Urteiler sollen n Objekte bewerten, indem sie sie in eine Rangreihe bringen. 

• Wenn alle Beurteiler zufällig urteilen, dann ist die Summe der zugewiesenen Urteilsränge ( Rangsummen) bei allen Objekten ungefähr gleich: = (m+2m+3m+...+nm)/n --> maximale Diskordanz. 

• Wenn sich die Beurteiler in allen Objekten 100% einig sind, dann betragen die Rangsummen 

  m, 2m, 3m,...,nm, wobei m die Rangsumme des Rang-ersten Objektes, nm die Rangsumme des rangletzten Objektes ist. ---> maximale Konkordanz. 

Je unterschiedlicher die Rangsummen der Objekte sind, desto höher ist die Konkordanz, desto eher stimmen die Beurteiler in ihren Urteilen überein. 

Das Devianzmass ist definiert durch folgende Quadratesumme: 

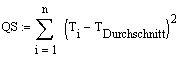
T_i: Rangsumme des i-ten Objektes 

T_durchschnitt: durchschnittliche Rangsumme (bei maximaler Diskordanz) 

Dieses Devianzmass muss noch an der maximal möglichen Quadratesumme (resultierend im Falle höchster Konkordanz: m, 2m, 3m,....,nm) relativiert werden, um es auf den Wertebereich [0...1] abzubilden.  

Daraus erhält man den Konkordanzkoeffizienten   

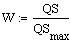  ,  bzw.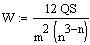  

In dieser Form werden Ties (Rangbindungen) jedoch nicht berücksichtigt.

Signifikanztest: 

Bei n>7 Objekten ist die Prüfgrösse W asymptotisch Chi-Quadrat verteilt mit n-1 Freiheitsgraden. 

Mit der Excelfunktion CHIVERT(Prüfgrösse, n-1) erhält man das einseitige Signifikanzniveau des Konkordanzkoeffizienten. 

Siehe auch Tabelle Korrelationskoeffizienten