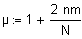Ohne Frames

Sequentieller Wald Wolfowitz Runs Test auf Zufälligkeit bei dichotomem Merkmal mit Excel Beispiel

oder Swed Eisenhart Test bzw. Steven's Iterationshäufigkeitstest  

Zuerst wird die normale, dann die sequentielle Testvariante beschrieben.

Im Gegensatz zum Iterationslängentest, der nur einen bestimmten, "verdächtigen" Teil einer Reihe testet, betrachtet der Iterationshäufigkeitstest bzw. Wald Wolfowitz Runs Test ( oder ... Run Test)die gesamte Reihe. Ein Run ist eine zusammenhängende, ununterbrochene Reihe gleichartiger Ausprägungen.

zurück zum Glossar (Wald Wolfowitz Runs Test)

Wald Wolfowitz Runs Test                                           Zum sequentiellen Iterationshäufigkeitstest (nach unten)

Auch unter den Namen Swed Eisenhart Test, Stevens' Iterationshäufigkeitstest bekannt. 

Testet eine Wertereihe dahingehend, ob die Wertereihenfolge zufällig ist oder nicht. 

Dieser Test detektiert Trends und Schwingungen. 

Bei diesem Test fragt man nach der Anzahl Runs bei alternativem Merkmal. 

Wenige Runs deuten auf Häufungen hin (z.B.: AAABBBBAAAAAAAABBBBB),  während viele Runs auf ein Schwingungsverhalten hindeuten (z.B.: ABABABAABABBA).

 

Voraussetzungen:  

-  keine Ausreisser, 

-  zu untersuchendes Merkmal ist dichotom oder notfalls dichotomisiert worden.

 

Beim Test wird die Anzahl sogenannter Runs gezählt, nachdem man alle Werte 2 möglichen Klassen zugeteilt hat (Dichotomisierung).

Der Test hat also binomialen Charakter.

Runs sind aus aufeinanderfolgenden Werten bestehende Teilgruppen,  welche der selben  Klasse angehören.

Klassen können z.B. sein:

Geht man die Wertereihe durch, dann ist die Wahrscheinlichkeit für einen Klassenwechsel bei zufälligem Zahlenmaterial nach jedem Wert immer 50%. 

Bei von vorne herein festgelegten unterschiedlichen Klassengrössen gilt dies natürlich nicht.

Der Erwartungswert für die Anzahl Runs bei einer Wertereihe der Länge N beträgt für den allgemeinen Fall unterschiedlicher Klassengrössen

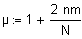Wald Wolfowitz Erwartungswert,  und die Standardabweichung Wald Wolfowitz Standardabweichung  

 

R: Anzahl Runs.

N: Gesamtanzahl Werte

n,m: Anzahl Werte in jeweils einer Klasse.

 

Die Prüfgrösse Wald Wolfowitz Teststatistik ist asymptotisch standardnormalverteilt [N(0,1)]. 

Bei N<60 sollte Stetigkeitskorrektur angewandt werden, d.h.: Im Zähler  von W sind 0,5 abzuziehen.

Für Stichprobengrössen < 20 gibt es tabellierte Schwellenwerte.

Diese Schwellenwerte berechnet man "exakt", das heisst: durch explizites Auszählen aller Möglichkeiten.

Betrachtungen dazu folgen am Ende dieser Rubrik.

 

Vorgehensweise: 

  1. Falls anwendbar: Mittelwert berechnen 

  2. Bestimmung der beiden Anzahlen Runs bezüglich beider Klassen sowie der Gesamtanzahl Einzelwerte. 

  3. Berechnen von Erwartungswert und Standardabweichung 

  4. Berechnen der Prüfgrösse und Vergleich mit Schwellenwerten. 

Beispiel: 

 

0.) Originaldaten: Warteschlange, Betrachtung der Geschlechtsreihenfolge. 

m m w w m w m m w w m w m w m w m m w m m w m w m

 

Nullhypothese: "Die Geschlechterreihenfolge ist zufällig"

 

1.) 

Mittelwertbildung nicht anwendbar. 

 

2.)

m m w w m w m m w w m w m w m w m m w m m w m w m
1 1     2   3 3     4   5   6   7 7   8 8   9   10
    1 1   2     3 3   4   5   6     7     7   9  

 

-> 10 + 9 = 19 Runs

Also N =25, R=19, n= 14, m= 11.

 

3.)

Erwartungswert der Anzahl Runs bei den gegebenen Daten: = 13.32

Standardabweichung der Anzahl Runs bei den gegebenen Daten: = 2.41

 

4.)

Prüfgrösse W= 2.15 mit Stetigkeitskorrektur. 

Berechnung der einseitigen Überschreitungswahrscheinlichkeit mit der Excelfunktion STANDNORMVERT(2.15)  liefert 98.4%. 

Da die Anzahl Runs (19) grösser ist als der Erwartungswert (13,32), folgt daraus, dass die Nullhypothese zum Signifikanzniveau 95% verworfen werden muss. 

 

Man interprätiert, dass sich die Geschlechter in der Reihe bei einem Signifikanzniveau von 98,4% "entmischt" haben. 

 

Anmerkungen zu exaktem Testen bei kleinen Stichproben.

 

Die Zahl der Iterationen (Runs) r1, r2, der beiden Klassen kann sich maximal um 1 unterscheiden, wie man durch Vergegenwärtigung einiger Beispiele leicht einsieht, also entweder

r1 =r2,         r1 = r2+1,         r1 = r2-1.

  1. AABABBAAA --> 3 A-Runs und 2 B-Runs

  2. BBBBAAABA -->  2 A-Runs und 2 B-Runs

  3. BABAB            --> 2 A-Runs und 3 B-Runs

Die Frage ist nun, wieviele mögliche Iterationen zu gegebenen r1, r2, n, m existieren.

Man stelle sich vor, die A's stehen bereits da, und die B's sind derart einzufügen, dass

  1. 3 A-Runs (also 2 B-Runs)

  2. 2 A-Runs (also 2 B-Runs) 

  3. 2 A-Runs (also 3 B-Runs)

entstehen.

  1. Durch Abzählen sieht man, dass es 4+3+2+1 = , allgemein: Möglichkeiten gibt.

    Weiterhin gibt es 2 Möglichkeiten, 3 B's auf 2 B-Runs zu verteilen, allgemein: .

Es gibt insgesamt also Möglichkeiten, n A's und m B's derart zu verteilen,

dass r1 A-Runs uns r2 B-Runs entstehen.

Relativiert man dies an der Anzahl Möglichkeiten, n A's und m B's ohne Einschränkungen anzuordnen:

, bzw. , so erhält man für die Punktwahrscheinlichkeit, n A's und m B's mit jeweils r1 bzw. r2 Runs anzuordnen:

  (r1 = r2+1  oder  r1 = r2-1).

2.     Analog erhält man für die Punktwahrscheinlichkeit im Falle r1 = r2 :

          (r1 = r2).

 

3.    Siehe 1.

 

Addiert man nun die Punktwahrscheinlichkeiten der betreffenden sowie aller noch unwahrscheinlicheren Kombinationen zusammen, so erhält man das exakte  Alpha Risiko (1 - Signifikanzniveau) der betreffenden Konstellation.

Die sequentielle Variante dieses Tests findet man hier. 

01.09.2005 

 

zurück zum Glossar (Wald Wolfowitz Runs Test) 

 

zurück zum Glossar (Sequentieller Iterationshäufigkeitstest)

 

 Sequentieller Iterationshäufigkeitstest

 

Sequentielle Variante des Wald Wolfowitz Runs Tests, jedoch mit einer sehr wesentlichen Einschränkung.

Siehe dazu die rot markierte Bemerkung in untenstehender Tabelle.

 

Bei diesem Test fragt man nach der Anzahl Runs bei alternativem Merkmal. 

Wenige Runs deuten auf Häufungen hin (z.B.: AAABBBBAAAAAAAABBBBB),  während viele Runs auf ein Schwingungsverhalten hindeuten (z.B.: ABABABAABABBA).

 

Für eine grundlegende Einführung in die Funktionsweise sequentieller Tests siehe sequentieller Binomialtest.

Dort werden auch die Gleichungen für die Annahmegeraden hergeleitet.

Beim sequentiellen Iterationshäufigkeitstest funktioniert diese Herleitung prinzipiell ähnlich.

Annahmegerade für die Nullhypothese H0:

Wald Wolfowitz Sequentiell H0 Annahme Gerade

 

 

 

 

Annahmegerade für die Alternativhypothese H1: 

Wald Wolfowitz Sequentiell H1 Annahme Gerade

 

Anmerkungen:

1. Die beiden Geradengleichungen unterscheiden sich nur in dem Glied, in dem a und b vorkommen.

 

2. Die "2"en im Nenner berücksichtigen die Tatsache, dass man nur nach der Häufigkeit Runs der einen Klasse sucht.

 

3. Dieser Test in Form der oben dargestellten Formeln macht zur Bedingung, dass unter der Nullhypothese H0 die Wahrscheinlichkeit für einen Klassenwechsel 0,5 ist.  Andere Werte als 0,5 sind nicht erlaubt.

Dies ist eine sehr wesentliche Einschränkung gegenüber der nicht-sequentiellen Testvariante.

 

4. d bedeutet die Abweichung von 0,5 unter der Alternativhypothese H1. Typischerweise wird d maximal zu +0,2 oder -0,2 angenommen.

x ist hier die abhängge Variable (Anzahl Runs der EINEN Klasse),

n die unabhängige Variable (Anzahl Testdurchläufe = Anzahl bisheriger  Individuen in BEIDEN Klassen zusammen).

09.01.2005

 

Beispielskizze (selbe Daten wie beim Wald Wolfowitz Runs Test) 

 

Originaldaten: Warteschlange, Betrachtung der Geschlechtsreihenfolge. 

m m w w m w m m w w m w m w m w m m w m m w m w m

 

Zunächst aus didaktischen Gründen das graphische Ergebnis des Beispiels Wald Wolfowitz Sequentiell Beispiel

 

x: Anzahl "männlicher" Iterationen (Wieviel Gruppen von Männern wurden gefunden, nachdem man bei der n-ten Person der Warteschlange angekommen ist?)

n: Anzahl Personen, die der Reihe nach untersucht worden sind.

 

Weitere Daten zu diesem Beispiel:

- Alpha- und Beta Risiko wurden jeweils zu 0,1 gesetzt.

- d wurde zu -0,1 angenommen (H1: d = -0,1)

- Achtung: p0 = 0,5, andernfalls kann dieser Test nicht angewandt werden (Siehe Anmerkung in rot, oben). 

 

Die Berechnung des zuvor genannten Beispiels in Excel befindet sich hier.

29.08.2005

zurück zum Glossar (Sequentieller Iterationshäufigkeitstest)

Datenschutzhinweise