Elektrischer Ohmscher Widerstand und Spannungsteiler für Laien

Spannungsteiler Grundlagen (1)

Wiederholung:

R = U/I    (1)

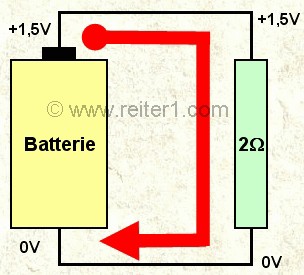
Das erste Bild zeigt einen geschlossenen Stromkreis mit einer Batterie als Quelle und einem Widerstand mit 2 Ohm, der einen Verbraucher symbolisieren soll.

Dargestellt ist eine 1,5V Batterie, Pluspol oben 1,5V, Minuspol unten, 0V.

Die Zuweisung des Wertes 0V zum Minuspol ist eine zunächst willkürlich erscheinende Festlegung. Rein mathematisch würde nichts dagegen sprechen, den Minuspol auf irgendeinen anderen Wert festzulegen, solange nur der Pluspol sich um 1,5 V nach oben davon unterscheidet.

Es erweist sich jedoch als praktisch, die Bezugsbasis auf 0V zu legen.

Der rote Pfeil symbolisiert Richtung und Stärke des fliessenden Stroms.

An den Batteriepolen sind die herrschenden Spannungswerte eingezeichnet. Rechts davon ober- und unterhalb des Widerstandes sind die selben Spannungswerte nochmal eingezeichnet, da wir naiverweise davon ausgehen, dass die Spannung entlang der Leitungen erhalten bleibt.

Später werden wir sehen, dass dies abhängig vom technischem Kontext nicht ganz stimmt.

Die eingezeichneten Spannungswerte suggerieren, dass entlang des Stromweges durch den Widerstand etwas mit der Spannung passieren muss. Es scheint so, als ob auf dem Weg durch den Widerstand die Spannung allmählich abnimmt.

Widerstände gibt es in unterschiedlichen Bauformen und Materialien, unter anderem auf Keramikkörper gewickelter Widerstandsdraht.

Dieses Drahtmaterial zeichnet sich dadurch aus, dass es kein perfekter Leiter ist, sondern einen definierten Widerstand pro Längeneinheit aufweist.

Je länger der Widerstandsdraht, desto grösser der Widerstand. Die Länge des Widerstandsdrahtes ist damit ein Mass für den Gesamtwiderstand, und den Widerstand einer bestimmten Drahtlänge könnte man auch mittels Aneinanderreihen von 2 halb so langen Drähten realisieren.

Genau diesen Sachverhalt stellt das nächste Bild dar.

Der 2Ω Widerstand wurde durch zwei 1Ω Widerstände ersetzt.

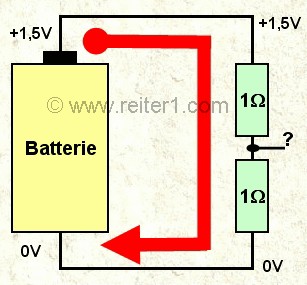
Der Gesamtwiderstand und der fliessende Strom sind gleich geblieben.

Welche Spannung wird man an dem Anzapfungspunkt zwischen den Widerständen messen?

Um dies herauszufinden bedarf es noch einer trivial erscheinenden Annahme, nämlich dass der Strom in einem geschlossenen unverzweigten Kreis an jeder Stelle gleich ist. Strom geht also nicht verloren.

Berechnen wir also zunächst den Strom I.

R = U/I nach I aufgelöst ergibt I = U/R.

Werte eingesetzt: I = 1,5V/2Ω = 0,75A.

Nun wenden wir die Formel blindlings nur auf den oberen Widerstand an. Dass man dies darf, wird im folgenden klar.

R= U/I nach U aufgelöst ergibt U = R x I.

Werte eingesetzt: U = 1Ω x 0,75A = 0,75V

Für den unteren Widerstand ergibt sich ganz analog ebenfalls 0,75V

Die Spannung fällt also im oberen Widerstand anscheinend von 1,5V um 0,75V auf 0,75V ab, und im unteren Widerstand fällt sie anscheinend von 0,75V um 0,75V auf 0V ab. Man nennt diesen Vorgang Spannungsabfall. Dass dies auch tatsächlich so ist, also dass man insbesondere U = R x I auf einen stromdurchflossenen Widerstand "einfach so" anwenden darf, wird im folgenden Kapitel experimentell gezeigt. Die Formel U = R x I suggeriert, dass der durchfliessende Strom die Ursache und die dabei entstehende Spannung die Wirkung ist, also umgekehrt wie an früherer Stelle dargelegt. Beide Sichtweisen sind richtig.

Weiter