Zurück zu statistische Hypothese
Diese Seite enthält die folgenden, aufeinander aufbauenden Rubriken:
Logische Aussage über eine Eigenschaft einer Grundgesamtheit, die man einem Test unterziehen will.
Da diese logische Aussage sich evtl. als falsch herausstellen kann, bezeichnet man die Aussage als Hypothese.
Diese Hypothese kann ein mathematischer Ausdruck oder eine eindeutige verbale Formulierung sein.
Beispiele:
| Hypothesenart | Beispiel einer maximal genauen Formulierung |
| Unspezifische Hypothese | a ungleich b |
| Spezifische Hypothese | a ist um 2 grösser als b |
| Ungerichtete Hypothese | a und b unterscheiden sich um 2 |
| Gerichtete Hypothese | a ist grösser als b |
| Zusammenhangshypothese | "a = 2*b" |
| Unterschiedshypothese | a >< b |
Alle in der Tabelle genannten Hypothesenarten haben weniger mathematischen, sondern eher sprachlichen Stellenwert.
Siehe auch das Beispiel unter Poweranalyse.
Die Hypothese wird mit H0, Nullhypothese, bezeichnet.
Das Gegenteil davon, also die "Gegenhypothese" dazu, wird mit H1, Alternativhypothese, bezeichnet.
Es ist also in der realen (unbekannten) Welt in jedem Fall entweder H0 oder H1 wahr.
In der Praxis jedoch
weiss man nie, ob H0 oder H1 richtig ist, weil man
lediglich eine Stichprobe der Grundgesamtheit zur Entscheidungsfindung heranzieht.
Letzteres ist Ursache dafür, dass der Testausgang, egal in welcher Richtung, mit einem Irrtumsrisiko behaftet ist.
Diese Risiken sind graphisch weiter unten und tabellarisch noch weiter unten in der Rubrik Risikoarten_bei_statistischen_Hypothesentests dargestellt.
Beispiele zu Hypothesenformulierungen
Zweiseitig (ungerichtet):
H0: Die durchschnittlichen Körpergrössen von Männern und Frauen sind gleich.
H1: Die durchschnittliche Körpergrösse von Männern ist anders (also grösser oder kleiner) als die von Frauen
Einseitig (gerichtet):
H0: Die durchschnittlichen Körpergrössen von Männern und Frauen sind gleich.
H1: Die durchschnittliche Körpergrösse von Männern ist grösser als die von Frauen
1. Einseitige statistische Hypothese, gerichtete statistische Hypothese
Angenommen, es existierte in Wirklichkeit kein Unterschied zwischen den Durchschnittsgrössen der Geschlechter.
Führte man wiederholt Stichproben durch und berechnete den sich aus den Stichproben ergebenden durchschnittlichen Grössenunterschied zwischen den Geschlechtern, dann würden die Ergebnisse irgendwie um Null verteilt sein, das heisst, manche Stichproben würden ergeben, dass Männer im Mittel grösser sind und wiederum andere würden ergeben, dass Frauen im Mittel grösser sind.
Über alle Stichproben betrachtet wäre aber der Bereich um Null (kein Grössenunterschied) der Wahrscheinlichste.
Folgendes Bild veranschaulicht die Verteilung des Stichprobenergebnisses .
Einseitig (gerichtet):
H0: Die durchschnittlichen Körpergrössen von Männern und Frauen sind gleich.
H1: Die durchschnittliche Körpergrösse von Männern ist grösser als die von Frauen
Zur Überprüfung der Hypothese erhebe man eine Stichprobe.
Wenn es -wie eingangs bemerkt- in Wirklichkeit keinen Unterschied zwischen den Durchschnittsgrössen der Geschlechter gäbe, dann würde das Stichprobenergebnis sehr wahrscheinlich eine Durchschnittsgrössendifferenz nahe bei Null ergeben.
Mit einer zwar kleinen, aber vorhandenen Wahrscheinlichkeit jedoch würde man eine Durchschnittsgrössendifferenz ermitteln, die "deutlich" von Null verschieden ist.
Der rote Flächenanteil in obigem Bild macht etwa 10% der Gesamtfläche der Wahrscheinlichkeitsverteilung des Stichprobenergebnisses aus. Dieser Bereich erscheint zunächst willkürlich gewählt, ergibt aber im weiteren Kontext einen Sinn
Mit einer Wahrscheinlichkeit von 10% fällt das Stichprobenergebnis in diesen Bereich.
Wenn das Stichprobenergebnis in diesen Bereich gefallen ist, dann sagt man:
"Die Nullhypothese (kein Unterschied zwischen den Geschlechtern) muss zum Signifikanzniveau von 90% (=100% -10%) verworfen werden", bzw.
Das Testergebnis ist zu >= 90% signifikant (je nachdem, wo genau im roten Bereich das Ergebnis liegt),
denn wenn es wirklich keinen Unterschied zwischen den Geschlechtern geben würde, dann würde man nur mit 10% Wahrscheinlichkeit ein Stichprobenergebnis bekommen, welches in den roten Bereich fällt.
Man
sieht an den bisherigen Formulierungen sehr deutlich, dass man aus der
Stichprobe eigentlich keinen quantitativen Schluss auf die wahre (aber
unbekannte) Welt ziehen kann, denn man geht ja immer von der Hypothese
selbst aus: "Wenn die Nullhypothese gilt, dann würde das
Stichprobenergebnis nur mit 10% Wahrscheinlichkeit so oder extremer
ausfallen". Die Wahrscheinlichkeit mit der die Nullhypothese an sich
zutrifft kann man aber nicht angeben, sie
ist nicht definiert.
Selbst
Wahrscheinlichkeiten in der Art "Wie oft würde man recht haben, wenn
man die Ergebnisse dieses statistischen Hypothesentests so-und-so
interpretiert", lassen sich nicht angeben.
Insbesondere
kann man nicht sagen, dass Männer mit 90% Wahrscheinlichkeit grösser
sind als Frauen, wenn der Testausgang im roten Bereich zu liegen kommt.
Genausowenig kann man sagen, dass man in 90% aller Fälle richtig liegen
würde, wenn man einen "roten" Testausgang als nichtzutreffende
Nullhypothese auffassen würde. Man kann lediglich sagen, dass, wenn H0
zutrifft, in einem von 10 Fällen mit einem "roten" Testausgang zu
rechnen ist.
Zu
quantitativen Schlussfolgerungen auf die reale Welt bedarf es neben der
expliziten H1 Formulierung noch einer weiteren Annahme. Siehe hierzu
weiter unten unter b).
Es gibt aber noch weitere Punkte, die man beachten muss:
Die Möglichkeit, dass Frauen im Schnitt grösser sein könnten als Männer wurde beim Testdesign gar nicht in Betracht gezogen (siehe zweiseitiges Testen weiter unten).
Es wurde keine Angabe gemacht, welchen Grössenunterschied man als relevant betrachtet. Theoretisch könnten Männer mit sehr hoher Signifikanz um ein Zehntel Millimeter grösser als Frauen sein. Obwohl statistisch signifikant, wäre dies praktisch irrelevant.
Warum wurde bisher der rote Bereich gerade im rechten Eck gewählt?
Weil man bei der Formulierung der Hypothesen
Einseitig (gerichtet):
H0: Die durchschnittlichen Körpergrössen von Männern und Frauen sind gleich.
H1: Die durchschnittliche Körpergrösse von Männern ist grösser als die von Frauen
bereits "insgeheim" in Betracht gezogen hat, dass Männer in Wahrheit durchschnittlich grösser sind als Frauen, oder etwas positiver formuliert:
Per fachmännischen Beschluss wurde von vorneherein ausgeschlossen, dass Frauen grösser sind als Männer.
Deswegen hat man die 10% Flächenanteil ganz nach rechts gelegt, weil es unter der Voraussetzung, Männer seien tatsächlich grösser als Frauen (das ist ja die Vermutung), leichter zu signifikanten Testergebnissen kommt (bei festgelegtem Signifikanzniveau, hier 90%).
"Vermutungen müssen immer sachlich begründet werden, idealerweise mittels unabhängiger Methoden.
2. Zweiseitige statistische Hypothese, ungerichtete statistische Hypothese
Alles zuvor unter der Rubrik "Einseitige Statistische Hypothese" Gesagte gilt auch hier.
Allerdings sei jetzt folgende Hypothese formuliert:
Zweiseitig (ungerichtet):
H0: Die durchschnittlichen Körpergrössen von Männern und Frauen sind gleich.
H1: Die durchschnittliche Körpergrösse von Männern ist anders (also grösser oder kleiner) als die von Frauen
Man erhebe wieder eine Stichprobe
Es gilt wieder alles unter der Rubrik "Einseitige Statistische Hypothese" Gesagte.
Der rote Flächenanteil in obigem Bild macht wieder etwa 10% der Gesamtfläche der Wahrscheinlichkeitsverteilung des Stichprobenergebnisses aus.
Dieser Bereich ist nun aber anders gewählt und erscheint zunächst wieder willkürlich, ergibt aber im weiteren Kontext einen Sinn.
Mit einer Wahrscheinlichkeit von 10% fällt das Stichprobenergebnis wieder in den roten Bereich.
Wenn das Stichprobenergebnis in diesen Bereich gefallen ist, dann sagt man wieder:
"Die Nullhypothese (kein Unterschied zwischen den Geschlechtern) muss zum Signifikanzniveau von 90% (=100% -10%) verworfen werden", bzw.
Das Testergebnis ist zu >= 90% signifikant (je nachdem, wo genau im roten Bereich das Ergebnis liegt)
Die
beiden Formulierungen entsprechen den Formulierungen weiter oben im einseitigen, gerichteten Fall.
In der Praxis folgert man wieder:
"Die durchschnittliche Körpergrösse zwischen den Geschlechtern ist zum Signifikanzniveau 90% nicht gleich".
Wieder dürfen die 90% hier nicht mit einer Wahrheitsaussage verwechselt werden.
Im Übrigen gelten hier die selben Schlussfolgerungen wie weiter oben beim einseitigen, gerichteten Fall.
Der grundlegende Unterschied zum einseitigen, gerichteten Fall besteht darin, dass in dieser (zweiseitig
formulierten) Hypothese im Vorhinein kein fachmännischer Beschluss
stattgefunden hat, bzw. keine spezifischeVermutung bestanden hat.
Aus diesem Grunde musste man die "extremsten" 10% denkbarer Stichprobenausgänge auf beide "Schwänze" der Wahrscheinlichkeitsverteilung verteilen.
Wenn nun in Wirklichkeit Männer im Durchschnitt grösser wären als Frauen, dann wäre in dieser zweiseitigen Hypothesenformulierung das Erreichen von Signifikanz erschwert, weil die Grenzen zu den roten Teilbereichen weiter von Null weg liegen als die Grenze der Fläche im einseitigen, gerichteten Fall.
Es ist wohl deutlich geworden, dass das einseitige Testen ohne vorausgehende fachmännische Vermutung eine geeignete Quelle für "statistisches Lügen" darstellt, weil es das Erreichen von signifikanten Ergebnissen erleichtert.
Zurück zu statistische Hypothese
05.11.2012
Zurück zu Anmerkungen zu statistischen Hypothesen
Anmerkung: Es ist ratsam, diese Seite von ganz oben nach unten durchzulesen
Anmerkungen zu statistischen Hypothesen
Statistische
Hypothesen müssen immer im Voraus formuliert werden, das heisst, vor
den Hypothesentests.
Nachträglich formulierte oder unüberprüfte Hypothesen sind ohne wissenschaftlichen Wert und -leider- eine weitere Quelle für statistische Lügen.
Es gibt auch statistische Methoden, welche vor der Formulierung statistischer Hypothesen angewandt werden; sie heissen hypothesegenerierende Verfahren. (--> explorative Datenanalyse).
a) Alternativhypothese ist lediglich Negation der Nullhypothese
Hypothesen (egal ob Null- oder Alternativ-) können verworfen oder nicht verworfen werden. Sie können jedoch nicht angenommen oder gar bestätigt werden.
Durch die Wahl eines Signifikanzniveaus, welches in der Regel bei 90% oder darüber liegt, geht man ja schon ein erhebliches Risiko ein, einen tatsächlich vorhandenen Sachverhalt gar nicht zu bemerken (Beta Risiko).
Man
stelle sich zum Beispiel vor, die Nullhypothese kann bei einem
geforderten Signifikanzniveau
von 90% nicht verworfen werden, weil das Datenmaterial lediglich für
ein Signifikanzniveau von 80% "ausreicht".
Es sei hier angemerkt, dass über das Beta Risiko nichts ausgesagt werden kann, da man nicht näher angibt, ein wie grosser Unterschied als relevant gelten soll. Es wird lediglich die Nullhypothese explizit formuliert. Sollte die Nullhypothese (in Wahrheit zurecht) verworfen werden müssen, dann kann man ohne Weiteres nichts über die Grösse des erkannten Unterschiedes aussagen. Man kann lediglich Aussagen machen über die Wahrscheinlichkeitsverteilung des erkannten Unterschiedes, aber bei diesem Ansinnen hätte man die Alternativhypothese gleich zu Anfang explizit formulieren können und den Test entsprechend führen können. Siehe dazu den nächsten Unterabschnitt b).
Bei einseitigen Hypothesenformulierungen sollte man wenigstens etwas fachliches Vorwissen haben.
In dem unter Statistische Hypothese genannten Beispiel vermutet man, dass Männer grösser sind als Frauen. Der Test soll nun offenbaren, ob diese Vermutung signifikant ist..
Bei einseitiger Hypothesenformulierung lässt man also eine Seite unbeachtet, was dazu führt, dass es auf der anderen Seite leichter zu Signifikanz kommt als es bei zweiseitiger Formulierung der Fall wäre.
Nachträgliche einseitige Formulierung ist übrigens ein geeignetes "Mittel", bei knapp verfehlter zweiseitiger Signifikanz doch noch (einseitige) Signifikanz herbeizuführen.
b) Explizite und eigenständige Formulierung der Alternativhypothese (Vollständige Formulierung, Neyman-Pearson Testtheorie)
Die effektivste Gestaltung eines Tests beinhaltet neben der Formulierung der Nullhypothese
(mit dem dazu gehörenden Alpha Risiko) zusätzlich
die explizite Formulierung der Alternativhypothese (mit dem zugehörigen Beta Risiko)
Daraus ergibt sich dann
die explizite Festlegung einer Effektgrösse, die die Nullhypothese von der Alternativhypothese klar trennt.
Hinweis: Alpha-, Betarisiko und Effektgrösse sind nicht alle frei wählbar. Durch Wahl von Zweien wird die dritte festgelegt.
Beispiel:
H0: Männer und Frauen sind im Mittel gleich gross.
H1: Männer sind im Schnitt mindestens 6 cm grösser als Frauen. (Effektgrösse = 6 cm)
Folgendes Bild verdeutlicht dies
Die blaue Kurve gibt die Verteilung der Stichprobenergebnisse wieder unter der Annahme, dass in Wahrheit die H0 gilt
(kein Unterschied zwischen den Geschlechtern).
Die rosa Kurve gibt die Verteilung der Stichprobenergebnisse wieder unter der Annahme, dass in Wahrheit die H1 "gerade noch" gilt (also das Wort "mindestens" durch "genau" ersetzt wird -> Männer im Schnitt genau 6 cm grösser als Frauen).
Die 6 cm in diesem Beispiel ist die Effektgrösse, also derjenige Mindestunterschied, der gefordert wird, um relevant zu sein.
Effektgrössen sind im Vorhinein auf Grundlage fachmännischer Kriterien festzulegen.
Es sei hier betont, dass die beiden Kurven die Verteilungen der Stichprobendurchschnitte darstellen, nicht die Verteilungen der Körpergrössen selbst. Erstere sind nach dem zentralen Grenzwertsatz deutlich schmäler als letztere, nämlich proportional zu n-1/2 .
Die hellgrüne senkrechte Linie schneidet die rechten 10% der Fläche unter der blauen Kurve ab und symbolisiert das Signifikanzniveau 90% bezüglich der Nullhypothese (->Alpha Risiko = 10%).
Von der Fläche unter der rosa Kurve schneidet die senkrechte grüne Linie nur ca. 1% links ab.
Dies symbolisiert das "Signifikanzniveau" 99% bezüglich der Alternativhypothese (->Beta Risiko = 1%)
Nun nehmen wir beispielhaft an, das Stichprobenergebnis sei genau auf die grüne Linie gefallen.
Dann bedeuten die letzten 3 Sätze konkret folgendes:
Wenn die H0 gilt, dann würde das Stichprobenergebnis
nur mit 10% Wahrscheinlichkeit eine derartige oder gar noch extremere
Ausprägung annehmen.
Wenn die H1 gilt, dann würde das Stichprobenergebnis
nur mit 1% Wahrscheinlichkeit eine derartige oder gar noch extremere
Ausprägung annehmen.
Legt man die grüne Linie weiter nach rechts, beispielsweise:
dann gilt (Zahlen sind geschätzt):
Wenn die H0 gilt, dann würde das Stichprobenergebnis nur mit 1% Wahrscheinlichkeit eine derartige oder gar noch extremere Ausprägung annehmen. -
Wenn die H1 gilt, dann würde das Stichprobenergebnis
nur mit 10% Wahrscheinlichkeit eine derartige oder gar noch extremere
Ausprägung annehmen.
Offensichtlich hat sich die "Erkennnungsstärke" der H0 erhöht zuungunsten der "Erkennungsstärke" der H1.
Man hat also zum besseren Erkennen einer in Wahrheit geltenden H0 die Empfindlichkeit des Erkennens einer in Wahrheit geltenden H1 verringert.
Hier wird deutlich, dass Alpha Risiko und Beta Risiko in Konkurrenz stehen. Will man beide Risiken minimieren, dann bleibt -abgesehen von der Vergrösserung der Effektgrösse- nur noch die Erhöhung der Stichprobengrösse.
In der Praxis wird man aber in der Regel einen Kompromiss eingehen. Dabei kann es von unterschiedlicher Wichtigkeit sein, einen tatsächlichen Unterschied möglichst sicher entdecken zu wollen, oder einen tatsächlich nicht vorhandenen Unterschied sicher erkennen zu wollen.
Im Gegensatz zu denjenigen Tests, bei denen sich die Alternativhypothese lediglich aus der Negierung der Nullhypothese ergibt (und das Beta Risiko in der Regel unbekannt bleibt, eine Effektgrösse erst gar nicht formuliert wird),
gibt es bei dieser Testform 2 eindeutige Ergebnisse:
Die Nullhypothese wird nicht verworfen, die Alternativhypothese dagegen schon,
genau umgekehrt.
Dies wird im Folgendenetwas näher beleuchtet.
Beispielsweise könnte der wahre durchschnittliche Grössenunterschied zwischen Männern und Frauen weder 0 noch 6, sondern z.B. genau 3 cm sein.
Je nach Lage des Signifikanzniveaus (bzw. Beta Risikos, grüne Linie) wird man aber immer entweder für 0 oder 6 cm entscheiden.
Ist man mit relativ hohem Alpharisiko zufrieden, dann wird man im Falle von wirklichen 3 cm für 6 cm entscheiden.
Verringert man das Alpharisiko, dann wird man im Falle von wirklichen 3 cm für 0 cm entscheiden.
Wählt man beide Risiken gleich, dann ist es in Falle von wirklichen 3 cm 50:50 Glückssache, ob der Test für 0 oder 6 cm ausgeht.
Daran ändert sich auch nichts, wenn man beide Risiken mittels Stichprobenvergrösserung beliebig klein macht.
Es ist also durchaus sinnvoll, sich für nur ein Risiko zu entscheiden und das andere Risiko bewusst grösser zu belassen.
Wäre es z.B. "schlimmer", einen evtl. wirklichen Unterschied von 6 cm zu übersehen, dann würde man alpha relativ gross belassen (z.B. 10%) und Beta relativ klein wählen (z.B.1%).
Man geht dann eben das Risiko ein, dass es bei einem für 6 cm signifikanten Testergebnis in Wahrheit nur z.B. 4 cm sind.
Ein wirklicher Sachverhalt von 6 cm würde sich darin äussern, dass das Alpha -Signifikanzniveau bei wiederholten Tests immer wieder sehr weit überschritten und selten bis nie unterschritten wird.
Man beachte, dass bei konventioneller Testform infolge des Fehlens einer expliziten eigenständigen Alternativhypothese es nur 2 "schwammige" Ergebnisse gab, die zudem noch anders zu formulieren sind:
Die Nullhypothese wird abgelehnt /verworfen,
Die Nullhypothese kann nicht abgelehnt / verworfen werden.
Welche quantitativen Aussagen sind jetzt über die wahre (aber unbekannte) Welt überhaupt möglich?
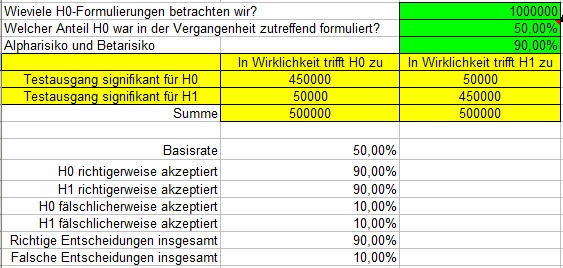
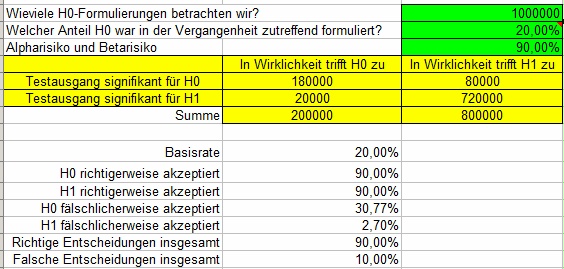
Falsche H1 sind relativ selten (20.000 von 20.000 + 720.000 = 2,7%), und sogar absolut selten.
Falsche H0 sind relativ häufig (80.000 von 80.000 + 180.000 = 30,77%), und sogar absolut häufig.
Interessanterweise sind die gesamten Anteile richtiger bzw. falscher Entscheidungen gleich geblieben.
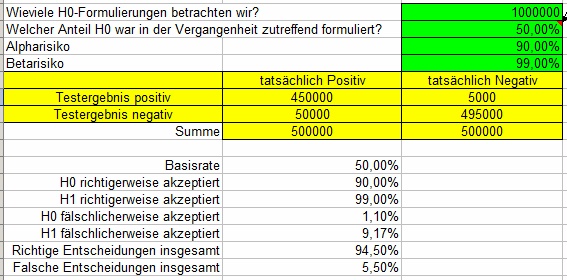
Die intuitive
Interpretation, wonach man bei z.B. 90% signifikantem Testausgang in
90% aller Fälle recht hätte, stimmt in jedem Fall, unabhängig, wieviel
fachliche Ahnung der Hypothesenformulierer hat, vorausgesetzt, die
Alternativhypothese wurde explizit formuliert, und ist nicht lediglich
die Verneinung der Nullhypothese.
Eine ganz besondere
Konsequenz ergibt sich, wenn man den Anteil richtiger H0 der
Vergangenheit sehr nahe bei 0 oder 100% wählt. In der medizinischen
Diagnostik ist dies der Realfall, mit der Konsequenz, dass positive
Testausgänge selbst bei sehr trennscharfem Test nur wenig Aussagekraft haben. Ein
etwaiger AIDS-Test an der gesamten deutschen Bevölkerung würde weitaus
mehr Falsch-Positive als Richtig-Positive hervorbringen. Siehe hierzu
die Exceldatei Praevalenz_und_Testergebnis.xls.
Beispiele für Tests mit expliziter Formulierung der Alternativhypothese und Festlegung einer Effektgrösse finden sich unter
Zurück zu Anmerkungen zu statistischen Hypothesen
05.11.2012
Zurück zu statistischer Hypothesentest
Anmerkung: Es ist ratsam, diese Seite von ganz oben nach unten durchzulesen
A priori Test, bei dem (im Gegensatz zur eplorativen Datenanalyse)
vorher formulierte statistische Hypothesen überprüft werden.
aufgrund des Informationsgehaltes von Stichproben Schlüsse auf die zugehörige Grundgesamtheit gezogen werden.
Diese Schlüsse sind mit einer genau zu definierenden Irrtumswahrscheinlichkeit behaftet.
Alle statistischen Hypothesentests berechnen eine so genannte Prüfgrösse, deren Wert unmittelbar über das Schicksal der Nullhypothese entscheidet.
Statistische Hypothesentests führt man deshalb durch, damit man nicht die gesamte Grundgesamtheit untersuchen muss (was oft unmöglich ist), sondern mit Stichproben arbeiten kann.
Bei statistischen Hypothesentests ist stets ein Abwägen vonnöten zwischen statistischer Unsicherheit und Aufwand des Tests.
Vorgehensweise:
(Verbale) Formulierung einer Hypothese, festlegen ob ein- oder zweiseitig.
Festlegen der Testparameter, entweder:
Signifikanzniveau (=1- Alpha Risiko) und Stichprobengrösse
-> das Beta Risiko ergibt sich daraus und ist oft leider nicht näher bekannt.
Signifikanzniveau, Beta Risiko und Effektgrösse.
-> die Stichprobengrösse ergibt sich daraus.
Durchführung des Tests, Ermittlung der Prüfgrösse.
Interpretation des Ergebnisses
Verwerfen oder Nicht-Verwerfen der Nullhypothese
Nullhypothese annehmen oder Alternativhypothese annehmen
Siehe auch Design eines zweiseitigen Tests als Beispiel.
Für einen Überblick über die wichtigsten statistischen Tests in Abhängigkeit des Skalenniveaus siehe hier.
Für einen allgemeineren Einstieg siehe Statistische Hypothese.
Für eine Auflistung sämtlicher in diesem Glossar vorkommenden Tests siehe hier.
Zurück zu statistischer Hypothesentest
05.11.2012
Zurück zu Risikoarten bei statistischen Hypothesentests
Anmerkung: Es ist ratsam, diese Seite von ganz oben nach unten durchzulesen
Risikoarten bei statistischen Hypothesentests
In folgender Tabelle sind die Risikoarten sowie weitere Kenngrössen statistischer Hypothesentests tabellarisch dargestellt.
Die
zum Teil redundanten Kenngrössenbezeichnungen stammen aus
unterschiedlichen Fachbereichen.
H0:
Patient ist gesund.
|
Verschiedene Begriffe über Risikoarten von Hypothesentests |
Reale Welt (unbekannt) |
||
| H0 trifft zu | H1 trifft zu | ||
|
Welt des Hypothesen- tests. H0: Patient sei krank |
Test ergibt H0 |
Signifikanzniveau, p-Wert, Konfidenzkoeffizient.
-Wirkt sich aus auf: Richtig negativ |
Alpha Risiko, Lieferantenrisiko, Überschreitungswahrscheinlichkeit. Risiko 1. Art
-Wirkt sich aus auf: Falsch positiv |
|
Test ergibt H1 |
Risiko 2. Art, Güte
-Wirkt sich aus auf: Falsch negativ |
Power, Konfidenzkoeffizient Trennschärfe, Teststärke Epsilon,
-Wirkt sich aus auf: Richtig positiv |
|
Anmerkung:
Hohe Signifikanzniveaus bedeuten zwar niedriges Alpha Risiko, also ein geringes Risiko, fälschlicherweise einen Sachverhalt zu erkennen.
Andererseits wird dadurch jedoch das Beta Risiko erhöht, also das Risiko, einen tatsächlich vorhandenen Sachverhalt nicht zu erkennen.
Alpha und Beta Risiko stehen somit in Konkurrenz zueinander.
Dieser Konkurrenz kann man nur durch Vergrössern der Stichprobe wirksam begegnen.
Zur weiteren Vertiefung des Themas "Risikoarten bei statistischen Tests" siehe
Diagnostische Tests: Medizinisch bedeutsame Kennwerte..
Zurück zu Risikoarten bei statistischen Hypothesentests
05.11.2012
Datenschutzhinweise